对于集合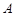 ,定义了一种运算“
,定义了一种运算“ ”,使得集合
”,使得集合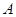 中的元素间满足条件:如果存在元素
中的元素间满足条件:如果存在元素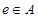 ,使得对任意
,使得对任意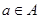 ,都有
,都有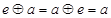 ,则称元素
,则称元素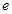 是集合
是集合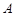 对运算“
对运算“ ”的单位元素.例如:
”的单位元素.例如: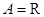 ,运算“
,运算“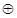 ”为普通乘法;存在
”为普通乘法;存在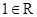 ,使得对任意
,使得对任意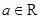 ,都有
,都有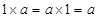 ,所以元素
,所以元素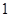 是集合
是集合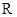 对普通乘法的单位元素.
对普通乘法的单位元素.
下面给出三个集合及相应的运算“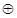 ”:
”:
①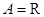 ,运算“
,运算“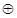 ”为普通减法;
”为普通减法;
②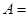 {
{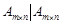 表示
表示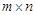 阶矩阵,
阶矩阵, },运算“
},运算“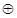 ”为矩阵加法;
”为矩阵加法;
③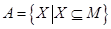 (其中
(其中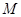 是任意非空集合),运算“
是任意非空集合),运算“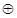 ”为求两个集合的交集.
”为求两个集合的交集.
其中对运算“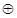 ”有单位元素的集合序号为
”有单位元素的集合序号为
| A.①② | B.①③ | C.①②③ | D.②③ |
已知等比数列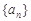 前
前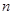 项和为
项和为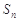 ,则下列一定成立的是
,则下列一定成立的是
A.若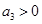 ,则 ,则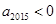 |
B.若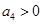 ,则 ,则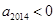 |
C.若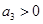 ,则 ,则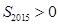 |
D.若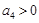 ,则 ,则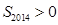 |
“ ”是“关于
”是“关于 的二元一次方程组
的二元一次方程组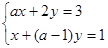 有唯一解”的
有唯一解”的
| A.必要不充分条件 |
| B.充分不必要条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
已知等比数列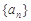 前
前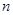 项和为
项和为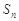 ,则下列一定成立的是
,则下列一定成立的是
A.若 ,则 ,则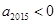 |
B.若 ,则 ,则 |
C.若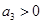 ,则 ,则 |
D.若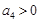 ,则 ,则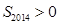 |
“ ”是“关于
”是“关于 的二元一次方程组
的二元一次方程组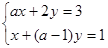 有唯一解”的
有唯一解”的
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |