复数 =( )
=( )
A.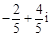 |
B.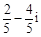 |
C. |
D. |
一只蚂蚁从长方体 的顶点
的顶点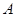 出发,沿着长方体的表面到达顶点
出发,沿着长方体的表面到达顶点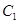 的最短距离为6,则长方体体积的最大值为()
的最短距离为6,则长方体体积的最大值为()
| A.24 | B.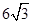 |
C.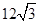 |
D.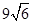 |
某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为()
A.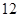 |
B.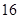 |
C.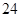 |
D.32 |
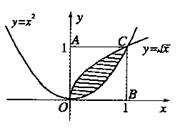
曲线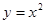 和曲线
和曲线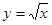 围成一个叶形图(如图所示阴影部分),其面积是()
围成一个叶形图(如图所示阴影部分),其面积是()
| A.1 | B.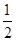 |
C.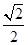 |
D.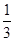 |
已知样本容量为30,在样本频率分布直方图(如图)中,各小长方形的高的比从左到右依次为2∶4∶3∶1,则第2组的频率和频数分别为()
| A.0.4,12 | B.0.6,16 | C.0.4,16 | D.0.6,12 |
阅读下面的程序框图,运行相应的程序,输出的结果为()
A. |
B. |
C. |
D. |