已知函数 .
.
(1)若函数 在
在 内单调递增,求
内单调递增,求 的取值范围;
的取值范围;
(2)若函数 在
在 处取得极小值,求
处取得极小值,求 的取值范围.
的取值范围.
为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草 如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形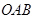 的顶点
的顶点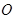 为圆心,
为圆心, 在圆周上,
在圆周上,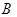 在半径
在半径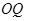 上,设计要求
上,设计要求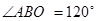

(1)请设置一个变量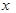 ,写出该蝶形区域的面积
,写出该蝶形区域的面积 关于
关于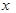 的函数表达式;
的函数表达式;
(2)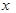 为多少时,该蝶形区域面积
为多少时,该蝶形区域面积 最大?
最大?
设椭圆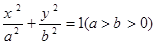 的左焦点为
的左焦点为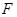 ,短轴上端点为
,短轴上端点为 ,连接
,连接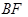 并延长交椭圆于点
并延长交椭圆于点 ,连接
,连接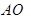 并延长交椭圆于点
并延长交椭圆于点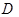 ,过
,过 三点的圆的圆心为
三点的圆的圆心为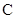
(1)若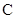 的坐标为
的坐标为 ,求椭圆方程和圆
,求椭圆方程和圆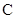 的方程;
的方程;
(2)若 为圆
为圆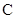 的切线,求椭圆的离心率
的切线,求椭圆的离心率
如图,四边形ABCD为正方形,PD⊥平面ABCD,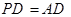 ,AF⊥PC于点F,FE∥CD交PD于点E.
,AF⊥PC于点F,FE∥CD交PD于点E.
(1)证明:CF⊥平面ADF;
(2)若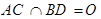 ,证明
,证明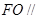 平面
平面
已知
(1)求 的值;
的值;
(2)求 的值
的值
已知实数 ,函数
,函数 .
.
(1)当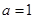 时,讨论函数
时,讨论函数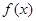 的单调性;
的单调性;
(2)若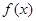 在区间
在区间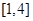 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若当 时,函数
时,函数 图象上的点均在不等式
图象上的点均在不等式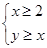 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数 的取值范围.
的取值范围.