如图,POQ是折成60°角的固定于竖直平面内的光滑金属导轨,导轨关于竖直轴线对称,OP=OQ=L.整个装置处在垂直导轨平面向里的足够大的匀强磁场中,磁感应强度随时间变化规律为B=B0-kt(其中k为大于0的常数).一质量为m、长为L、电阻为R、粗细均匀的导体棒锁定于OP、OQ的中点a、b位置.当磁感应强度变为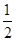 B0后保持不变,同时将导体棒解除锁定,导体棒向下运动,离开导轨时的速度为v.导体棒与导轨始终保持良好接触,导轨电阻不计,重力加速度为g.求导体棒:
B0后保持不变,同时将导体棒解除锁定,导体棒向下运动,离开导轨时的速度为v.导体棒与导轨始终保持良好接触,导轨电阻不计,重力加速度为g.求导体棒: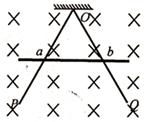
⑴解除锁定前回路中电流的大小及方向;
⑵滑到导轨末端时的加速度大小;
⑶运动过程中产生的焦耳热.
一物快以一定的初速度沿足够长的斜面向上滑动,其速度大小随时间的变化关系图如图所示,取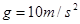 ,求:
,求:
(1)物快上滑过程和下滑过程的加速度大小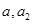 ;
;
(2)物快向上滑行的最大距离 ;
;
(3)斜面的倾角 .
.
(9分)如图所示,在光滑水平面上有一块长为L的木板B,其上表面粗糙.在其左端有一个光滑的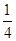 圆弧槽C与长木板接触但不连接,圆弧槽的下端与木板的上表面相平,B、C静止在水平面上.现有很小的滑块A以初速度v0从右端滑上B并以
圆弧槽C与长木板接触但不连接,圆弧槽的下端与木板的上表面相平,B、C静止在水平面上.现有很小的滑块A以初速度v0从右端滑上B并以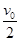 的速度滑离B,恰好能到达C的最高点.A、B、C的质量均为m,试求:
的速度滑离B,恰好能到达C的最高点.A、B、C的质量均为m,试求: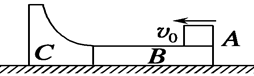
①木板B上表面的动摩擦因数μ.
②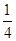 圆弧槽C的半径R.
圆弧槽C的半径R.
(9分)如图所示,一束截面为圆形(半径R=1 m)的平行紫光垂直射向一半径也为R的玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区.屏幕S至球心的距离为D=(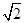 +1) m,不考虑光的干涉和衍射,试问:
+1) m,不考虑光的干涉和衍射,试问:
①若玻璃半球对紫色光的折射率为n=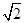 ,请你求出圆形亮区的半径.
,请你求出圆形亮区的半径.
②若将题干中紫光改为白光,在屏幕S上形成的圆形亮区的边缘是什么颜色?
(9分)如图所示,玻璃管粗细均匀(粗细可忽略不计),竖直管两封闭端内理想气体长分别为上端30cm、下端27cm,中间水银柱长10cm。在竖直管如图位置接一水平玻璃管,右端开口与大气相通,用光滑活塞封闭5cm长水银柱。大气压p0=75cmHg。
①求活塞上不施加外力时两封闭气体的压强各为多少?
②现用外力缓慢推活塞恰好将水平管中水银全部推入竖直管中,求这时上下两部分气体的长度各为多少?
如图所示,在第一、二象限存在场强均为E的匀强电场,其中第一象限的匀强电场的方向沿x轴正方向,第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场,矩形区域的AB边与x轴重合。M点是第一象限中无限靠近y轴的一点,在M点有一质量为m、电荷量为e的质子,以初速度v0沿y轴负方向开始运动,恰好从N点进入磁场,若OM=2ON,不计质子的重力,试求: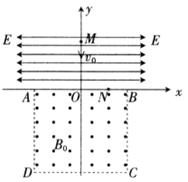
(1)N点横坐标d;
(2)若质子经过磁场最后能无限靠近M点,则矩形区域的最小面积是多少;
(3)在(2)的前提下,该质子由M点出发返回到无限靠近M点所需的时间。