如图甲所示,平行正对金属板中心线O处有一粒子源,能连续不断发出质量为m、电量为q、速度为v0的带正电的粒子,所有粒子均沿两板中心线射入板间,在紧靠板的上方等腰三角形PQR内有一垂直纸面向里的匀强磁场,三角形的对称轴与两板中心线重合,且∠RPQ=30°.两板间不加电压时粒子进入磁场时轨迹恰好与PR边相切,如图中所示.当在两板间加如图乙所示的周期性变化的电压时,t=0时刻进入板间的粒子恰好能从板边缘进入磁场.已知板长为l,板间距离为2d,PQ长度为6d,不计粒子的重力和粒子间的相互作用.求: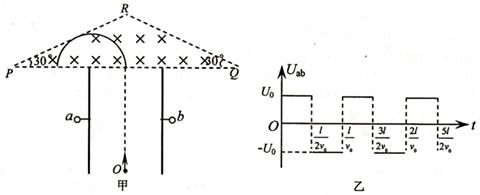
⑴磁感应强度B的大小;
⑵两板间电压U0;
⑶粒子在磁场中运动的最长和最短时间.
如图所示,轻质弹簧的劲度系数为20N/cm,用其拉着一个重200N的物体在水平面上运动.当弹簧的伸长量为4cm时,物体恰在水平面上做匀速直线运动.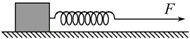
(1)求物体与水平面间的动摩擦因数;
(2)当弹簧的伸长量为6cm时,物体受到的水平拉力有多大?这时物体受到的摩擦力有多大?
(3)如果在物体运动的过程中突然撤去弹簧,而物体在水平面上能继续滑行,这时物体受到的摩擦力有多大?
一列从车站开出的火车,在平直轨道上做匀加速直线运动,已知这列火车的长度为L,火车头经过某路标时的速度为v1,而车尾经过此路标时的速度为v2,求:
(1)火车的加速度a.
(2)火车中点经过此路标时的速度v.
(3)整列火车通过此路标所用的时间t.
汽车以10m/s的速度在平直公路上匀速行驶,刹车后经2s速度变为6m/s,求:
(1)刹车过程中的加速度及刹车4s后的速度?
(2)刹车后8s内前进的距离
(3)停止运动前2s内的位移.
如图所示,放在水平面上质量为m的物体受一个斜上的拉力F,这个力与水平方向成θ角,在此力作用下,物体水平向右匀速滑动,求: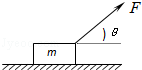
(1)物体与水平面间的动摩擦因数μ.
(2)如果把此力F撤去,此时物体做什么运动?摩擦力多大?
(3)如果在本题中已知动摩擦因数μ,现只给物体施加一个与水平方向成θ角的斜向下的推力F′,物体仍能保持匀速运动,求F′多大?
如图所示,重为100N的物体受推力F作用贴于墙面静止,F与墙的夹角θ=60°,墙对物体的最大静摩擦力为40N,要使物体保持静止,求推力F的大小范围.