麦克斯韦在1865年发表的《电磁场的动力学理论》一文中揭示了电、磁现象与光的内在联系及统一性,即光是电磁波.
一单色光波在折射率为1.5的介质中传播,某时刻电场横波图象如图甲所示,求该光波的频率.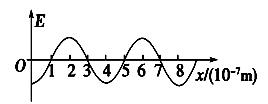
如图所示,用不可伸长的细线将重为G的球挂在光滑的竖直墙壁上静止时,求:线的拉力及墙对球的支持力的大小(线与竖直墙壁的夹角为θ).
如图所示,水平面上A、B两点相距x0=0.1m.甲球从B点向右做匀速运动的同时,乙球从A点由静止向右做匀加速运动,到达B点后以B点的速度匀速运动.乙球从开始运动,到追上甲球所用的时间t=1s,运动的位移x=0.9m,求;
(1)甲球的速度;
(2)乙球加速过程所用的时间和加速度.
某电视剧制作中心要拍摄一特技动作,要求特技演员从某大楼顶自由下落到行驶的汽车上,下落h时经过点P,此时从距地面高为H的Q点无初速度释放小物体,结果小物体和演员同时落在汽车上,不计空气阻力,重力加速度为g,求:
(1)P和Q中,哪一点位置高;
(2)PQ间的高度差.
一物体做匀加速直线运动,初速度为0.5m/s,第7s内的位移比第5s内的位移多4m,求:
(1)物体的加速度;
(2)物体在5s内的位移.
测速仪安装有超声波发射和接收装置,如图所示,B为测速仪,A为汽车,两者相距335m,某时刻B发出超声波,同时A由静止开始做匀加速直线运动.当B接收到反射回来的超声波信号时,A、B相距355m,已知声速为340m/s,求汽车的加速度大小.