图甲是中国自行设计、研制的最大的受控核聚变实验装置：其原理如图乙，带电粒子被强电流线圈产生的磁场约束在一个半经为r的“容器”中，通电线圈产生的圆形磁场可看作匀强磁场，磁场圆半径为R，R>r且两圆同心，磁感应强度为B,它们的截面如图丙所示。“容器”中有质量均为m，带电量均为q的带电粒子，在“容器”内运动， 有些粒子会运动到“容器”的边缘，观察到在“容器”的边缘各处，有向各个方向离开“容器”的粒子，且每个方向的粒子的速度都从0到v分布。不久，所有粒子都能返回“容器”。 （本题只考虑运动方向与磁场垂直的粒子，不计粒子重力和粒子间相互作用和碰撞）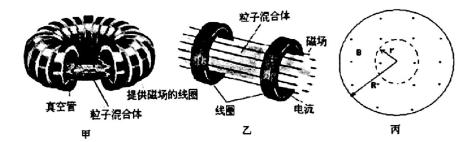
⑴要产生如图乙所示的磁场，逆着磁场方向看，线圈中的电流方向如何？不改变装置结构，要改变磁场，可釆取什么方法？
（2）为保证所有粒子从“容器”边缘处离开又能返回，求带电粒子的最大速度v
（3）如果“容器”中带电粒子是核聚变的原料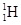
、
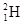，它们具拥同的动能，但被该装置约束后，它们的“容器”半径会不同。现用该装置约束这两种粒子，设它们“容器”的最大的半径分别为r1、r2，试推导r1、r2和R应满足的关系式。
一棱镜的截面为直角三角形ABC，∠A＝30°，斜边AB＝a.棱镜材料的折射率为n＝
.在此截面所在的平面内，一条光线以45°的入射角从AC边的中点M射入棱镜．画出光路图，并求光线从棱镜射出的点的位置(不考虑光线沿原路返回的情况)．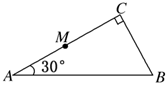
如图所示为波源O振动1.5 s时沿波的传播方向上部分质点振动的波形图．已知波源O在t＝0时开始沿y轴负方向振动，t＝1.5 s时它正好第二次到达波谷．问：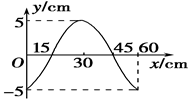
(1)再经过多长时间x＝5.4 m处的质点第一次到达波峰？
(2)从t＝0开始至x＝5.4 m处的质点第一次到达波峰这段时间内，波源通过的路程是多少？
已知锌板的极限波长λ0＝372 nm.今用处于n＝2激发态的氢原子发出的光照射锌板，已知氢原子能级公式En＝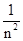
E1，E1＝－13.6 eV，电子质量me＝9.1×10－31 kg，问：
(1)氢原子发出光子的能量多大；
(2)锌板发生光电效应时，光电子的最大初动能是多少；
(3)具有最大初动能的电子对应的德布罗意波长多大．
如图所示，光滑的曲面轨道的水平出口跟停在光滑水平面上的平板小车的上表面相平，质量为m的小滑块从光滑轨道上某处由静止开始滑下并滑下平板小车，使得小车在光滑水平面上滑动．已知小滑块从光滑轨道上高度为H的位置由静止开始滑下，最终停到板面上的Q点．若平板小车的质量为3m．用g表示本地的重力加速度大小，求：
（1）小滑块到达轨道底端时的速度大小v0；
（2）小滑块滑上小车后，平板小车可达到的最大速度V；
（3）该过程系统产生的总热量Q．
质量为m="0.1" kg的小钢球从h1="5" m高处自由下落，与地板碰撞后上升h2="1.8" m，设碰撞时间t=0.2s，求钢球对地板的平均冲力. （g=10m/s2）