如图所示,匀强磁场B1垂直于光滑金属导轨平面向里,导体棒ab在平等于导轨的接力F作用下做匀加速运动,使电压表计数保持U不变。已知变阻器最大阻值为R1,定值电阻阻值为R2,平行金属板MN相距为d。一个带电荷量为+q,质量为m的粒子,由静止开始从O1加速经O2小孔垂直AC边射入匀强磁场区。已知该磁场的磁感应强度为B2,方向垂直纸面向外,其边界AD距O1O2的连线的距离为h。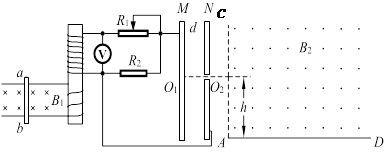
(1)R1的滑动头位于最右端时,MN两极间电场强度多大?
(2)调节R1的滑动头,使MN间电压为U时,粒子进入B2磁场后击中AD边界,求粒子在磁场中沿AD边界方向的射程S。(不计粒子重力)
(3)判断拉力F能否为恒力以及F的方向(不需要说明理由)
如图,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆ab,其下端(b端)距地面高度h=0.8 m.一质量为1kg的带电小环套在直杆上,正以某速度沿杆匀速下滑,小环离杆后正好通过b端的正下方c点处.(取b为零势能点,g取10 m/s2),求: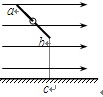
(1)小环离开直杆后运动的加速度大小和方向.
(2)小环在直杆上运动时的动能.
(3)小环从b到c运动过程中的机械能最小值.
如图所示,一传送装置可将货物从楼下传送到楼上,将货物轻放在传送带A端,被加速到B端后货物将沿着半径R=0.4m的光滑圆轨道运动经C点到达楼上。圆轨道与传送带B点相切,其中OC为圆轨道的半径且沿竖直方向,O点为圆轨道的圆心。已知传送带与货物间的动摩擦因数μ=0.8,传送带与水平面夹角θ=37°。已知sin37°=0.6,cos37°=0.8,g=10m/s2,货物可视为质点。求:
(1)货物在传送带上的加速度大小;
(2)传送带AB段 至少要多长?
2004年,中国正式开展月球探测工程,并命名为“嫦娥工程”,古老的月球即将留下中华儿女的足迹, 现宇航员欲乘航天飞机对在距月球表面高h处的圆轨道上运行的月球卫星进行维修.试根据你所学的知识回答下列问题:
(1)维修卫星时航天飞机的速度应为多大?
(2)已知地球自转周期为T0,则该卫星每天可绕月球转几圈?(已知月球半径为R,月球表面的重力加速度为gm,计算过程中可不计地球引力的影响,计算结果用h、R、gm、T0等表示)
如图所示,绝缘细线长为L,最大张力为T,一端固定于O点,另一端连接一带电荷量为q,质量为m的带正电小球,若T>mg,求: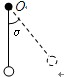
(1)若要小球保持静止,可在O点放置一带电量为多少的点电荷;
(2)若要小球静止时细线与竖直方向成α角,需叠加匀强电场的最小电场强度E为多大.
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内、管口B、C的连线是水平直径,现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R,从小球进入管口开始,整个空间中突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点,设小球运动过程中带电量没有改变,重力加速度为g,求:
(1)小球到达B点的速度大小;
(2)小球受到的电场力的大小和方向;
(3)小球经过管口C处时对圆管壁的压力。