如图所示，水平放置的足够长的平行金属导轨MN、PQ的一端接有电阻R0，不计电阻的导体棒ab静置在导轨的左端MP处，并与MN垂直．以导轨PQ的左端为坐标原点O，建立直角坐标系xOy，Ox轴沿PQ方向．每根导轨单位长度的电阻为r．垂直于导轨平面的非匀强磁场磁感应强度在y轴方向不变，在x轴方向上的变化规律为：B＝B0＋kx，并且x≥0．现在导体棒中点施加一垂直于棒的水平拉力F，使导体棒由静止开始向右做匀加速直线运动，加速度大小为a．设导体棒的质量为m，两导轨间距为L．不计导体棒与导轨间的摩擦，导体棒与导轨接触良好，不计其余部分的电阻．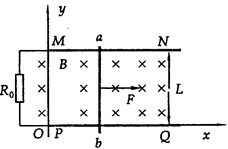
（1）请通过分析推导出水平拉力F的大小随横坐标x变化的关系式；
（2）如果已知导体棒从x＝0运动到x＝x0的过程中，力F做的功为W，求此过程回路中产生的焦耳热Q；
（3）若B0＝0．1T，k＝0．2T／m，R0＝0．1Ω，r＝0．1Ω／m，L＝0．5m，
a＝4m／s2，求导体棒从x＝0运动到x＝1m的过程中，通过电阻R0的电荷量q．
在光滑的水平面内，一质量m="1" kg的质点以速度v0="10" m/s沿x轴正方向运动，经过原点后受一沿y轴正方向上的水平恒力F="15" N作用，直线OA与x轴成α=37°角，如图所示曲线为质点的轨迹图(g取10 m/s2,sin37°=0.6,cos37°=0.8)，求：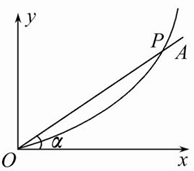
(1)如果质点的运动轨迹与直线OA相交于P点，质点从O点到P点所经历的时间以及P点的坐标；
(2)质点经过P点的速度大小。
某电视台的娱乐节目中，有一个拉板块的双人游戏，考验两人的默契度．如图所示，一长L=0.60m、质量M=0.40kg的木板靠在光滑竖直墙面上，木板右下方有一质量m=0.80kg的小滑块（可视为质点），滑块与木板间的动摩擦因数为μ=0.20，滑块与木板间的最大静摩擦力等于滑动摩擦力，取g=10m/s2．一人用水平恒力F1向左作用在滑块上，另一人用竖直恒力F2向上拉动滑块，使滑块从地面由静止开始向上运动．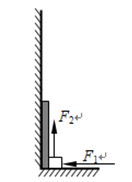
（1）为使木板能向上运动，求F1必须满足什么条件？
（2）若F1=22N，为使滑块与木板能发生相对滑动，求F2必须满足什么条件？
（3）游戏中，如果滑块上移h=1.5m时，滑块与木板没有分离，才算两人配合默契，游戏成功．现F1=24N，F2=16N，请通过计算判断游戏能否成功？
将质量为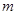
的木块放在倾角为
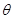的斜面上，木块恰可沿斜面匀速下滑。现用一沿斜面的恒力F作用于木块，使之沿斜面向上做匀加速运动，如图所示，求木块的加速度。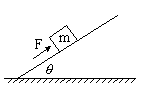
如图，质量m为5kg的物块(看作质点)在外力F1和F2的作用下正沿某一水平面向右做匀速直线运动。已知F1大小为50N,方向斜向右上方，与水平面夹角
，F2大小为30N,方向水平向左,物块的速度
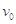大小为11m/s.当物体运动到距初始位置距离
时，撤掉F1，
（1）求物块与水平地面之间的动摩擦因数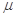
；
（2）求撤掉F1以后，物块在6S末距初始位置的距离。
如图所示，质量M=3Kg的物块A放在水平桌面上，物块A与桌面的动摩擦因数为μ=0.2，一轻绳跨过光滑的定滑轮连接A和B两个物块，物块B的质量m=1Kg，托起物块B，使物块B距离地面的高度h=0.5m，且轻绳刚好拉直。先由静止释放物块B，已知水平桌面足够长，物块A不会与滑轮相撞，g=10m/s2, 求：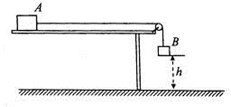
（1）B落地前物块A的加速度大小；
（2）物块A的运动总时间。