节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(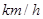 )分成六段
)分成六段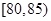 ,
,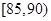 ,
,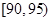 ,
,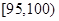 ,
,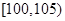 ,
,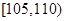 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)请直接回答这种抽样方法是什么抽样方法?并估计出这40辆车速的中位数;
(2)设车速在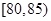 的车辆为
的车辆为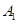 ,
,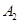 , ,
, ,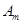 (
(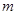 为车速在
为车速在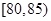 上的频数),车速在
上的频数),车速在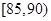 的车辆为
的车辆为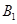 ,
,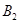 , ,
, ,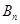 (
(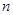 为车速在
为车速在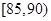 上的频数),从车速在
上的频数),从车速在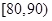 的车辆中任意抽取
的车辆中任意抽取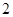 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的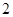 辆车的车速都在
辆车的车速都在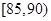 上的概率.
上的概率.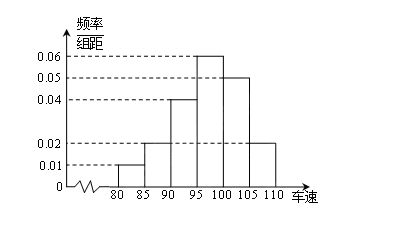
设函数 的定义域是
的定义域是 ,其中常数
,其中常数 .
.
(1)若 ,求
,求 的过原点的切线方程.
的过原点的切线方程.
(2)当 时,求最大实数
时,求最大实数 ,使不等式
,使不等式 对
对 恒成立.
恒成立.
(3)证明当 时,对任何
时,对任何 ,有
,有 .
.
设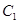 :
: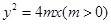 的准线与
的准线与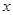 轴交于点
轴交于点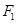 ,焦点为
,焦点为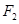 ;椭圆
;椭圆 以
以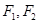 为焦点,离心率
为焦点,离心率 .设
.设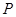 是
是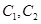 的一个交点.
的一个交点.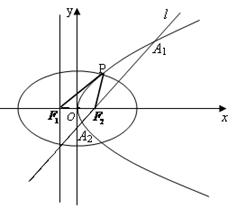
(1)当 时,求椭圆
时,求椭圆 的方程.
的方程.
(2)在(1)的条件下,直线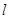 过
过 的右焦点
的右焦点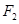 ,与
,与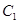 交于
交于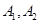 两点,且
两点,且 等于
等于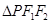 的周长,求
的周长,求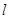 的方程.
的方程.
(3)求所有正实数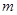 ,使得
,使得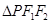 的边长是连续正整数.
的边长是连续正整数.
设 ,用
,用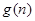 表示
表示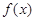 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数.
(1)求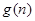 的表达式.
的表达式.
(2)设 ,求
,求 .
.
(3)设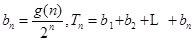 ,若
,若 ,求
,求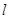 的最小值.
的最小值.
如图,正方体 中,已知
中,已知 为棱
为棱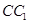 上的动点.
上的动点.
(1)求证: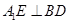 ;
;
(2)当 为棱
为棱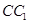 的中点时,求直线
的中点时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知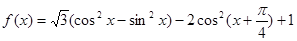 的定义域为[
的定义域为[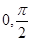 ].
].
(1)求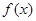 的最小值.
的最小值.
(2)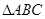 中,
中,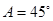 ,
, ,边
,边 的长为函数
的长为函数 的最大值,求角
的最大值,求角 大小及
大小及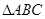 的面积.
的面积.