对实数a与b,定义新运算“⊗”: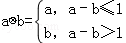 .设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A.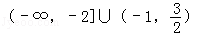 |
B.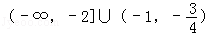 |
C.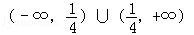 |
D.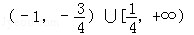 |
执行如图所示的程序框图,则输出的S值是( )
| A.﹣1 | B.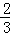 |
C.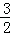 |
D.4 |
直线2x﹣3y+1=0的一个方向向量是( )
| A.(2,﹣3) | B.(2,3) | C.(﹣3,2) | D.(3,2) |
数列{an}的首项为3,{bn}为等差数列且bn=an+1﹣an(n∈N*),若b3=﹣2,b10=12,则a8=( )
| A.0 | B.3 | C.8 | D.11 |
设变量x,y满足约束条件: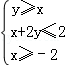 ,则z=x﹣3y的最小值( )
,则z=x﹣3y的最小值( )
| A.﹣2 | B.﹣4 | C.﹣6 | D.﹣8 |
已知f(x)=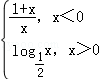 ,则f(x)≥﹣2的解集是( )
,则f(x)≥﹣2的解集是( )
A.(﹣∞,﹣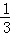 ]∪[4,+∞) ]∪[4,+∞) |
B.(﹣∞,﹣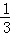 ]∪(0,4] ]∪(0,4] |
C.(﹣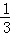 ,0]∪[4,+∞) ,0]∪[4,+∞) |
D.(﹣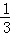 ,0]∪(0,4] ,0]∪(0,4] |