图中为“验证牛顿第二定律”的实验装置示意图。盘和重物的总质量为m,小车和砝码的总质量为M。实验中用盘和重物总重力的大小作为细线对小车拉力的大小。
①实验中,为了使细线对小车的拉力等于小车所受的合外力,先调节长木板一端定滑轮的高度,使细线与长木板平行。接下来还需要进行的一项操作是 (填写所选选项的序号)。
A.将长木板水平放置,让小车连着已经穿过打点计时器的纸带,给打点计时器通电,调节m的大小,使小车在盘和重物的牵引下运动,从打出的纸带判断小车是否做匀速运动。
B.将长木板的右端垫起适当的高度,让小车连着已经穿过打点计时器的纸带,撤去盘和重物,给打点计时器通电,轻推小车,从打出的纸带判断小车是否做匀速运动。
C.将长木板的右端垫起适当的高度,撤去纸带以及盘和重物,轻推小车,观察判断小车是否做匀速运动。
②实验中要进行质量m和M的选取,以下最合理的一组是 。
A.M=20g,m=10g、15g、20g、25g、30g、40g
B.M=200g,m=20g、40g、60g、80g、100g、120g
C.M=400g,m =10g、15g、20g、25g、30g、40g
D.M=400g,m ="20" g、40g、60g、80g、100g、120g
③图中是实验中得到的一条纸带,A、B、C、D、E、F、G为7个相邻的计数点,量出相邻的计数点之间的距离分别为x1、x2、x3、x4、x5、x6。已知相邻的计数点之间的时间间隔为T,关于小车的加速度a的计算方法,产生误差较小的算法是 。
A.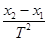
B.
C.
D.
如图所示,现有半导体热敏电阻R1、电炉丝、电源、电磁继电器、滑动变阻器、开关和导线若干。试设计一个温控电路:要求闭合开关后,温度超过某一温度时,电炉丝自动断电;低于某一温度时,又可以自动通电加热。
(1)请在图上连线,将热敏电阻R1接入电路。
(2)如果要求当温度更高时,电炉丝自动断电,则滑动变阻器的滑动触头应该向(填“左”或“右”)移动。
某同学用如图所示的装置做“验证动量守恒定律”的实验,先将球a从斜槽轨道上某固定点处由静止开始滚下,在水平地面的记录纸上留下压痕,重复10次,再把同样大小的球b放在斜槽轨道水平段的最右端处静止,让球a仍从原固定点由静止开始滚下,且与b球弹性相碰,碰后两球分别落在记录纸上的不同位置,重复10次.(两球都是在斜槽末端处的O点正上方水平飞出,且ma>mb)
(1)本实验必须测量的物理量是.( )(填序号字母)
A. 小球a、b的质量ma、mb
B. 小球a、b的半径r
C. 斜槽轨道末端到水平地面的高度H
D. 球a的固定释放点到斜槽轨道末端的高度差h
E. 小球a、b离开轨道后做平抛运动的飞行时间
F. 记录纸上O点到两小球的平均落点位置A、B、
C的距离 、
、 、
、
(2)放上被碰小球,两球(ma>mb)相碰后,小球a、b的平均落点位置依次是图中点和点.
(3)利用该实验测得的物理量,也可以判断两球碰撞过程中机械能是否守恒.判断的依据是看 与在误差允许范围内是否相等.
与在误差允许范围内是否相等.
某班同学在做“利用单摆测重力加速度”的实验中,
(1)如测出摆线长为 ,小球直径为D,
,小球直径为D, 次全振动的时间为
次全振动的时间为 ,则当地的重力加速度
,则当地的重力加速度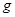 等于(用以上字母表示),为了减小测量周期的误差,应在位置开始计时和结束计时.
等于(用以上字母表示),为了减小测量周期的误差,应在位置开始计时和结束计时.
(2) 如果单摆的偏角小于50,某小组测得的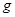 值偏小,可能原因是( )
值偏小,可能原因是( )
| A.单摆的振幅较小 |
| B.测摆线长时摆线拉得过紧 |
| C.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度稍微增加了 |
| D.开始计时时,秒表过迟按下 |
E.实验中误将49次全振动计为50次
(3)为了提高实验精度,在实验中可改变几次摆长 并测出相应的周期T,从而得出一组对应的
并测出相应的周期T,从而得出一组对应的 和T的数值,再以
和T的数值,再以 为横坐标、为纵坐标将所得数据连成直线,并求得该直线的斜率
为横坐标、为纵坐标将所得数据连成直线,并求得该直线的斜率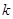 .则重力加速度
.则重力加速度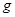 = (用
= (用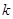 表示)
表示)
请完成以下两小题。(1)某同学在家中尝试验证平行四边形定则,他找到三条相同的橡皮筋(遵循胡克定律)和若干小事物,以及刻度尺、三角板、铅笔、细绳、白纸、钉字,设计了如下实验:将两条橡皮筋的一端分别在墙上的两个钉子A、B上,另一端与第二条橡皮筋连接,结点为O,将第三条橡皮筋的另一端通过细胞挂一重物。
①为完成实验,下述操作中必需的是。
a.测量细绳的长度b.测量橡皮筋的原长
c.测量悬挂重物后像皮筋的长度 d.记录悬挂重物后结点O的位置
②钉子位置固定,欲利用现有器材,改变条件再次实验证,可采用的方法是
某实验小组采用图示的装置探究“恒力拉动下小车的运动情况”,图中小车中可放置砝码,实验中,小车碰到制动装置时,钩码尚未到达地面,打点针时器工作频率为50 Hz.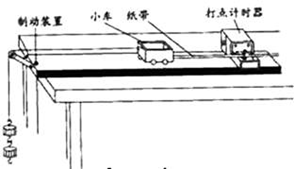
(1)实验的部分步骤如下,请将步骤②补充完整:
①在小车中放入砝码,把纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
②将小车停在打点计时器附近,,,小车拖动纸带,打点计时器在纸带上打下一系列点,断开开关,取下纸带。
③改变钩码或小车中砝码的数量,更换纸带,重复②的操作。
(2)下图是钩码质量为0.03 kg,砝码质量为0.02 kg时得到的一条纸带,在纸带上选择起始点0及A、B、C、D和E五个计数点,通过数据处理可获得各计数点对应时刻小车的瞬时速度v,
下表是纸带的一些测量结果,根据上面的插图可知OA的长度cm,OC的长度cm;
根据下表的数据可知,打下计数点C时,小车的瞬时速度是m/s。
| 测量点 |
S/cm |
v/(m·s-1) |
| 0 |
-- |
0.35 |
| A |
0.40 |
|
| B |
-- |
0.45 |
| C |
||
| D |
-- |
0.54 |
| E |
-- |
0.60 |
(3)由纸带和测量数据不难看出,纸带的(“左”或“右”)端是系小车的。