鸵鸟是当今世界上最大的鸟,由于翅膀退化它已经不会飞了。鸟起飞的必要条件是空气对它向上的力f足够大,计算f大小的公式为:f=cρSv2,式中c是一个无量纲的比例常数,ρ是空气密度,S是鸟翅膀的面积,v是鸟起飞时的速度。为了估算鸟起飞时的速度v,可以作一个简单的几何相似性假设:设鸟的几何线度为l,则鸟的质量与l3成正比,翅膀的面积S与l2成正比。已知燕子起飞时的速度约为20km/h,鸵鸟的几何线度大约是燕子的25倍。由此可估算出若要使鸵鸟能起飞,鸵鸟的速度必须达到
| A.50km/h | B.100km/h | C.200km/h | D.500km/h |
给滑块一初速度v0使它沿光滑斜面向上做匀减速运动,加速度大小为 ,当滑块速度大小变为
,当滑块速度大小变为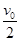 时,所用时间可能是( )
时,所用时间可能是( )
A. |
B. |
C. |
D. |
如图所示将一光滑的半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块。今让一小球自左侧槽口A的正上方从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是:()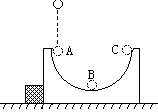
| A.小球在半圆槽内运动的全过程中,动量守恒 |
| B.小球在半圆槽内运动的全过程中,小球与半圆槽在水平方向动量守恒 |
| C.小球自半圆槽的最低点B向C点运动的过程中,小球与半圆槽在水平方向动量守恒 |
| D.小球离开C点以后,将做竖直上抛运动。 |
在距地面高为h,同时以相等初速V0分别平抛,竖直上抛,竖直下抛一质量相等的物体m,当它们从抛出到落地时,比较它们的动量的增量△P,有()
| A.平抛过程较大 | B.竖直上抛过程较大 | C.竖直下抛过程较大 | D.三者一样大 |
如图在光滑水平面上叠放AB两物体,其间有摩擦,mA=2 kg,mB=1 kg,速度的大小均为v0=10 m/s,设A板足够长,当观察到B做加速运动时,A的可能速度为( )
| A.2 m/s | B.3 m/s | C.4 m/s | D.5 m/s |
两名质量相等的滑冰人甲和乙都静止在光滑的水平冰面上.现在,其中一人向另一个人抛出一个篮球,另一人接球后再抛回.如此反复进行几次后,甲和乙最后的速率关系是( )
| A.若甲最先抛球,则一定是v甲>v乙 | B.若乙最后接球,则一定是v甲>v乙 |
| C.只有甲先抛球,乙最后接球,才有v甲>v乙 | D.无论怎样抛球和接球,都是v甲>v乙 |