如图所示,质量为m的小球从四分之一光滑圆弧轨道顶端静止释放,从轨道末端O点水平抛出,击中平台右下侧挡板上的P点。以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程 y=6-x2(单位:m),小球质量m="0.4" kg,圆弧轨道半径R=1.25m,g 取10 m/s2;求:
(1)小球对圆弧轨道末端的压力大小;
(2)小球从O点到P点所需的时间(结果可保留根号)。
如图所示,传送带与地面的倾角θ=37°,从A端到B端长度为L="16" m,传送带以v="10" m/s的速度沿逆时针方向转动.在传送带上端A处无初速地放置一个质量为0.5 kg的物体,它与传送带之间的动摩擦因数μ=0.5,求物体从A端运动到B端所需的时间是多少?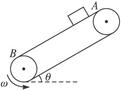
(sin37°=0.6,cos37°=0.8,取g="10" m/s2)
如图所示,质量M="10" kg的斜面体静止于粗糙的水平地面上,动摩擦因数μ=0.02,斜面的倾角θ=30°,一个质量m="1" kg的物体由静止开始沿斜面下滑,当滑行路程s="1.4" m时,其速度v="1.4" m/s,在此过程中斜面未动.求地面对斜面体的摩擦力的大小和方向.(取g="10" m/s2)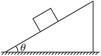
一木箱质量为m,与水平地面间的动摩擦因数为μ,现用斜向右下方与水平方向成θ角的力F推木箱,求经过t秒时木箱的速度.
质量为8 kg的木块放在粗糙的水平面上,在2 N的水平拉力作用下从静止开始做匀加速直线运动,经5 s位移是2.5 m.求:木块与地面间的动摩擦因数.
如图所示的电路中,定值电阻R="3" Ω,当开关S断开时,电源内、外电路消耗的功率之比为1∶3;当开关S闭合时,内、外电路消耗的功率之比为1∶1,求开关S闭合前和闭合后,灯泡L上消耗的功率之比(不计灯泡电阻的变化)。