如图所示，相距3L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场I的场强方向竖直向下，PT下方的电场II的场强方向竖直向上，电场I的场强大小是电场Ⅱ的场强大小的两倍，在电场左边界AB上有点Q，PQ间距离为L。从某时刻起由Q以初速度v0沿水平方向垂直射入匀强电场的带电粒子，电量为＋q、质量为m。通过PT上的某点R进入匀强电场I后从CD边上的M点水平射出，其轨迹如图，若PR两点的距离为2L。不计粒子的重力。试求：
（1）匀强电场I的电场强度E的大小和MT之间的距离；
（2）有一边长为a、由光滑弹性绝缘壁围成的正三角形容器，在其边界正中央开有一小孔S，将其置于CD右侧且紧挨CD边界，若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无机械能和电量损失)，并返回Q点，需在容器中现加上一个如图所示的匀强磁场，粒子运动的半径小于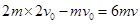
，求磁感应强度B的大小应满足的条件以及从Q出发再返回到Q所经历的时间。
在半径R＝5 000 km的某星球表面，宇航员做了如下实验，实验装置如图甲所示．竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m＝0.2 kg的小球，从轨道AB上高H处的某点由静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示．求：
(1)圆轨道的半径及星球表面的重力加速度．
(2)该星球的第一宇宙速度．
(3)从轨道AB上高H处的某点由静止释放小球，要使小球不脱离轨道，H的范围是多少？
在水平地面上固定一倾角θ＝37°、表面光滑的斜面体，物体A以v1＝6 m/s的初速度沿斜面上滑，同时在物体A 的正上方，有一物体B以某一初速度水平抛出，如图所示，如果当A上滑到最高点时恰好被B物体击中．(A、B均可看做质点，sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2)求：
(1)物体A上滑到最高点所用的时间t；
(2)物体B抛出时的初速度v2；
(3)物体A、B之间初始位置的高度差h.
(12分)如图所示，一质量为M的长木板静止在水平面上，有一质量为m的小滑块以一定的水平速度冲上木板，已知滑块和木板之间的动摩擦因数为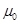
，最大静摩擦力等于滑动摩擦力，求
（1）若滑块在木板上滑动时，木板能保持静止不动，木板和地面之间的动摩擦因数须满足什么条件？
（2）若长木板的质量M=0.2kg，长木板与水平面间的动摩擦因数μ=0.1.滑块的质量也为0.2kg。滑块以v0=1.2m/s的速度滑上长板的左端，小滑块与长木板间的动摩擦因数μ0=0.4.滑块最终没有滑离长木板，求滑块在开始滑上长木板到最后静止下来的过程中，滑块滑行的距离是多少？（g=10m/s2）
某同学为了测定木块与斜面间的动摩擦因数，他用测速仪研究木块在斜面上的运动情况，装置如图甲所示。他使木块以初速度v0=4m/s的速度沿倾角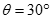
的斜面上滑，紧接着下滑至出发点，并同时开始记录数据，结果电脑只绘出了木块从开始上滑至最高点的v-t图线如图乙所示。g取10m/s2。求：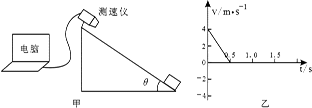
（1）上滑过程中的加速度的大小a1；
（2）木块与斜面间的动摩擦因数μ；
（3）木块回到出发点时的速度大小v。
如图所示，质量m= 2.0kg的木块静止在水平面上，用大小F="20" N、方向与水平方向成θ=37°角的力拉动木块，当木块运动到x=10m时撤去力F。不计空气阻力。已知木块与水平面间的动摩擦因数µ=0.2，sin37° =0.6，cos37°=0.8。g取10m/s2。求：
（1）撤去力F时木块速度的大小；
（2）撤去力F后木块运动的时间。