如图所示,一个匝数n=100、边长L=0.1m的正方形导线框abcd,以v=1m/s的速度向右匀速进入磁感应强度B=0.5T的匀强磁场,在运动过程中线框平面始终与磁场垂直,已知线框的总电阻R=25Ω。求在进入磁场的整个过程中
(1)导线中感应电流的大小;
(2)ab边所受安培力的大小;
(3)线框中产生的热量。
用伏安法测一节干电池的电动势E和内电阻r,所给的器材有:
| A.电压表V:0~3~15V; | B.电流表A:0~0.6~3A; |
| C.滑动变阻器R1:(总阻值20Ω); | D.滑动变阻器R2:(总阻值100Ω); |
E.电键S和导线若干。
(1)电压表量程选用_______;滑动变阻器选用______(填R1或R2);
(2)在虚线框中将电压表连入实验电路中;
(3)在U-I图中已画出七组实验数据所对应的坐标点,请根据这些点做出U-I图线并由图线求出:E=_________V,r=________Ω;
(4)在实验时,如果你连接的实物电路出现了如下问题:当开关闭合时发现电压表有示数 而电流表没有示数。如果在实验前仪器都检查过没有问题,只可能是与仪器连接的导线断了。请你判断一下,可能发生断路故障的导
而电流表没有示数。如果在实验前仪器都检查过没有问题,只可能是与仪器连接的导线断了。请你判断一下,可能发生断路故障的导 线是______(写出可能发生断路故障的导线的编号)。
线是______(写出可能发生断路故障的导线的编号)。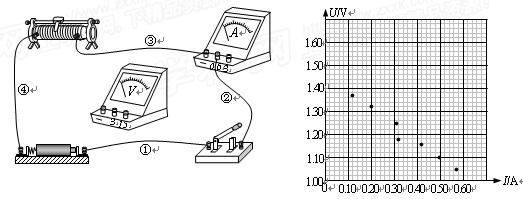
(1)一条纸带与做匀加速直线运动的小车相连,通过打点计时器打下一系列点,从打下的点中选取若干计数点,如图中A、B、C、D、E所示,纸带上相邻的两个计数点之间有四个点未画出。现测出AB=2.20cm,AC=6.40cm,AD=12.58cm,AE=20.80cm,已知打点计时器电源频率为50Hz。回答下列问题:
①打D点时,小车的速度大小为_______m/s;
②小车运动的加速度大小为_______m/s2。(①②均保留两位有效数字)
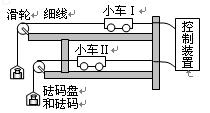
(2)在“探究加速度与物体质量、物体受力的关系”活动中,某小组设计了如图所示的实验装置。图中上下两层水平轨道表面光滑,两小车前端系上细线,细线跨过滑轮并挂上砝码盘,两小车尾部细线连到控制装置上,实验时通过控制装置使两小车同时开始运动,然后同时停止。本探究实验是通过比较两小车的位移来比较小车加速度的大小。能进行这样的比较,是因为:_______________________
_____________________________________________。
如图所示是一张羽毛和苹果在真空中下落的频闪照片,照片中显示的现象说明了:___________________________________________________________________________________。
在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图5所示,用米尺测量金属丝的长度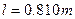 。金属丝的电阻大约为4Ω。先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该
。金属丝的电阻大约为4Ω。先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该 金属材料的电阻率。
金属材料的电阻率。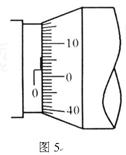
(1)从图5中读出金属丝的直径为______________。
(2)在用伏安法测定金属丝的电阻时,除被测的电阻丝外,还有如下供选择的实验器材:
直流电源:电动势约4.5V,内阻很小;
电流表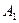 :量程0~0.6A,内阻0.125Ω;
:量程0~0.6A,内阻0.125Ω;
电流表 :量程0~3.0A,内阻0.025Ω;
:量程0~3.0A,内阻0.025Ω;
电压表V:量程0~3V,内阻3kΩ;
滑动变阻器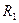 :最大阻值10Ω;
:最大阻值10Ω;
滑动变阻器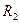 :最大阻值50Ω;
:最大阻值50Ω;
开关、导线等。
在可供选择的器材中,应该选用的电流表是_______________,应该选用的滑动变阻器是_______________________。
(3)根据所选的器材,画出实验电路图。
(4)若根据伏安法测出电阻丝的电阻为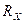 =4.1Ω,则这种金属材料的电阻率为____________Ω·m。(保留二位有效数字)
=4.1Ω,则这种金属材料的电阻率为____________Ω·m。(保留二位有效数字)
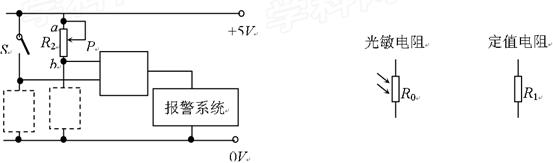
下图是用一个逻辑电路、电键S、安装在室外的光敏电阻R0、定值电阻R1和滑动变阻器R2组成的报警系统控制电路。该控制系统的功能是:工作日的晚上(光线较暗),报警系统自动开始工作;非工作日只要合上电键S,报警系统24小时都能工作(报警系统工作时,逻辑电路输出端为高电位)。
在两个虚线框内分别画上光敏电阻或定值电阻,并在实线框内标上门电路的符号,该门电路 是________门电路。
是________门电路。