光电效应和康普顿效应深入地揭示了光的粒子性的一面。前者表明光子具有能量，后者表明光子除了具有能量之外还具有动量。由狭义相对论可知，一定的质量m与一定的能量E相对应：
，其中c为真空中光速。
（1）已知某单色光的频率为ν，波长为λ，该单色光光子的能量
，其中h为普朗克常量。试借用质子、电子等粒子动量的定义：动量=质量×速度，推导该单色光光子的动量
。
（2）光照射到物体表面时，如同大量气体分子与器壁的频繁碰撞一样，将产生持续均匀的压力，这种压力会对物体表面产生压强，这就是“光压”，用I表示。
一台发光功率为P0的激光器发出一束某频率的激光，光束的横截面积为S。当该激光束垂直照射到某物体表面时，假设光全部被吸收，试写出其在物体表面引起的光压的表达式。
（3）设想利用太阳光的“光压”为探测器提供动力，将太阳系中的探测器送到太阳系以外，这就需要为探测器制作一个很大的光帆，以使太阳光对光帆的压力超过太阳对探测器的引力，不考虑行星对探测器的引力。
一个质量为m的探测器，正在朝远离太阳的方向运动。已知引力常量为G，太阳的质量为M，太阳单位时间辐射的总能量为P。设帆面始终与太阳光垂直，且光帆能将太阳光一半反射，一半吸收。试估算该探测器光帆的面积应满足的条件。
如图所示，绝缘细线一端固定于O点，另一端连接一带电荷量为q，质量为m的带正电小球，要使带电小球静止时细线与竖直方向成а角，可在空间加一匀强电场则当所加的匀强电场沿着什么方向时可使场强最小?最小的场强多大?这时细线中的张力多大?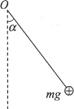
扭摆器是同步辐射装置中的插入件，能使粒子的运动轨迹发生扭摆，其简化模型如图所示：I、II两处的条形匀强磁场区域的宽度分别为L1、L2，边界竖直，I区域的右边界和II区域的左边界相距L，磁感应强度大小分别为B1、B2，方向相反且垂直纸面。一质量为m、电量为－q、重力不计的粒子，从靠近平行板电容器的负极板处由静止释放，两极板间电压为U，粒子经电场加速后平行纸面射入I区域，射入时的速度方向与水平方向的夹角θ＝30°。
（1）当L1＝L，B1＝B0时，粒子从I区域右边界射出时速度与水平方向的夹角也为30°，求B0及粒子在I区域中运动的时间t1；
（2）若L2＝L1＝L，B2＝B1＝B0，求粒子在I区域中的最高点与II区域中的最低点之间的高度差h；
（3）若L2＝L1＝L，B1＝B0，为使粒子能返回I区域，求B2应满足的条件；
（4）若L1≠L2，B1≠B2，且已保证粒子能从II区域的右边界射出，为使粒子从II区域右边界射出时速度与从I区域左边界射入时的方向总相同，求B1、B2、L1、L2之间应满足的关系式。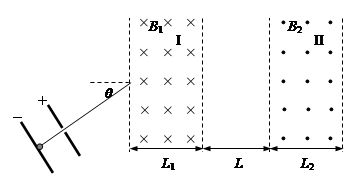
如图所示，竖直放置的半圆形光滑绝缘轨道半径为R，圆心为O，最高点为D，下端与绝缘水平轨道在B点平滑连接。一质量为m、带电量为+q的小物块置于水平轨道上的A点。已知A、B两点间的距离为L，小物块与水平轨道间的动摩擦因数为μ，重力加速度为g。
（1）若物块能到达的最高点是半圆形轨道上与圆心O等高的C点，则物块在A点水平向左的初速度应为多大？
（2）若整个装置处于方向竖直向上的匀强电场中，物块在A点水平向左的初速度vA=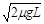
，沿轨道恰好能到达最高点D，并向右飞出，则匀强电场的场强E多大？
（3）若整个装置处于方向水平向左、场强大小E′=
的匀强电场中，现将物块从A点由静止释放，
运动过程中始终不脱离轨道，求物块第2n（n＝1、2、3……）次经过B点时的速度大小。
篮球比赛时，为了避免对方运动员的拦截，往往采取将篮球与地面发生一次碰撞后传递给队友的方法传球——击地传球。设运动员甲以v0＝5m/s 的水平速度将球从离地面高 h1＝0.8m处抛出，球与地面碰撞后水平方向的速度变为原来水平速度的4/5，竖直方向离开地面瞬间的速度变为与地面碰前瞬间竖直方向速度的3/4，运动员乙恰好在篮球的速度变为水平时接住篮球。运动员与篮球均可看成质点，篮球与地面发生作用的时间为0.02s，并认为篮球与地面接触时可看成是水平方向的匀变速运动，不计空气阻力，g取10m/s2，求甲抛球的位置与乙接球的位置之间的水平距离。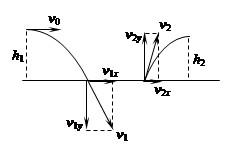
如图所示，倾角θ = 60°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，轻弹簧一端固定，自由端在B点，整个轨道处在竖直平面内。现将一质量为m的小滑块（视为质点）紧靠且压缩弹簧，并从导轨上离水平地面高h =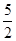 
R的A处无初速下滑进入圆环轨道，恰能到达圆环最高点D，不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5，重力加速度大小为g。求：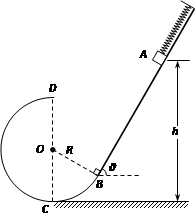
（1）滑块运动到圆环最高点D时速度υD的大小；
（2）滑块运动到圆环最低点时受到圆环轨道支持力N的大小；
（3）滑块在A处时弹簧的弹性势能Ep。