已知某商品的进价为每件40元，售价是每件60元，每星期可卖出-优题课

（本小题满分8分）如果代数式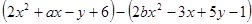的值与字母x所取的值无关，试求代数式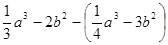的值．

（本小题满分8分）课外数学小组的女同学原来占全组人数的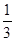，后来又有4个名女同学加入，就占全组人数的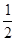，问课外数学小组原来有多少名同学？

（本小题满分10）某服装公司一周计划生产1000套服装，平均每天生产200套．由于各种原因实际每天生产的服装数量与比计划数量有多有少，下表是某周的生产情况（超产为正，减产为负，单位：套）：

星期	一	二	三	四	五
增减	＋5	－10	－4	－2	＋13

（1）根据记录可知前3天共生产套．
（2）产量最多的一天比产量最少的一天多生产套．
（3）公司规定每生产一套服装付工资80元，超额完成任务每套奖20元，少生产一套扣20元，那么该厂工人这一周的工资总额是多少?

（本小题满分6分）阅读下面例题的解题过程，再解答后面的题目．
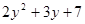例题已知代数式，求的值．
解：由
得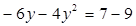
即，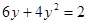
因此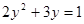，所以．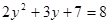
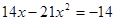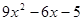问题已知代数式，求的值．

（本小题满分8分）方程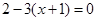的解与关于x的方程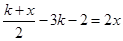的解互为倒数，求k的值．