如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
线 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为 , .
①求 关于 的函数表达式;
②当 时,求 的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
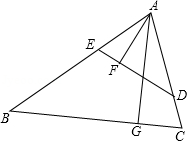
如图,在锐角三角形 中,点 , 分别在边 , 上, 于点 , 于点 , .
(1)求证: ;
(2)若 , ,求 的值.
在平面直角坐标系中,一次函数 , 都是常数,且 的图象经过点 和 .
(1)当 时,求 的取值范围;
(2)已知点 在该函数的图象上,且 ,求点 的坐标.
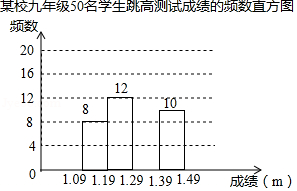
为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
|
组别 |
频数 |
|
|
8 |
|
|
12 |
|
|
|
|
|
10 |
(1)求 的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在 (含 以上的人数.
如图,在射线 , , , 围成的菱形 中, , , 是射线 上一点, 与 , 都相切,与 的延长线交于点 .过 作 交线段 (或射线 于点 ,交线段 (或射线 于点 .以 为边作矩形 ,点 , 分别在围成菱形的另外两条射线上.
(1)求证: .
(2)设 ,当矩形 的面积为 时,求 的半径.
(3)当 或 与 相切时,求出所有满足条件的 的长.
