阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.
小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
如果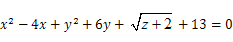 ,求
,求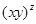 的值.
的值.
阅读理解:一个分数,如果分子加上9,结果是 ;如果分子加上4,结果是
;如果分子加上4,结果是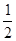 .求原来这个分数.
.求原来这个分数.
解:设这个分数为 ,则,
,则,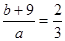 ,
, .
. .
.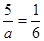 .
. .
.
所以原来这个分数是 .
.
请你根据对上面计算方法的理解,解答下题:
一个分数,如果分子加上2,结果是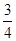 ;如果分子减去3,结果是
;如果分子减去3,结果是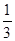 .
.
求原来这个分数.
甲、乙两辆汽车分别从A、B两地同时相向而行.已知甲车行完全程需要8小时,乙车行完全程需要6小时,如果两车各行3小时,两车之间的距离占全程的几分之几?如果两车各行4小时,两车之间的距离占全程的几分之几?
预备年级四个班的人数如图所示: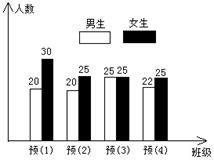
(1)男生人数占全年级人数的几分之几?
(2)女生人数占全年级人数的几分之几?
(3)预备(2)班人数是预备(1)班人数的几分之几?
一本书共有200页,小丽第一天看了全书的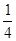 ,第二天看了全书的
,第二天看了全书的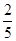 .
.
求:(1)小丽两天看了多少页?
(2)小丽还剩几分之几没看?