在平面直角坐标系xOy中，直线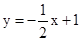
分别与x轴，y轴交于过点A，B，点C是第一象限内的一点，且AB=AC，AB⊥AC，抛物线
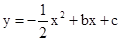经过A，C两点，与
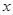轴的另一交点为D．
（1）求此抛物线的解析式；
（2）判断直线AB与CD的位置关系，并证明你的结论；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A,B,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
计算：
计算：
如图，四边形ABCD是梯形，
，PC是抛物线的对称轴，且
.
（1）求抛物线的函数表达式；
（2）求点D的坐标；
（3）求直线AD的函数表达式；
（4）PD与AD垂直吗？
正方形ABCD的边长为8，正方形EFGH的边长为3，正方形EFGH可在线段AD上滑动. EC交AD于点M. 设AF=x，FM=y，△ECG的面积为s.
（1）求y与x之间的关系；
（2）求s与x之间的关系；
（3）求s的最大值和最小值；
（4）若放宽限制条件，使线段FG可在射线AD上滑动，直接写出s与x之间的关系.
如图，∠C=90°，∠CAE=∠ABC，AC=2，BC=3.
（1）判断AE与⊙O的位置关系，并说明理由；
（2）求OB的长；