如图，在Rt△ABC中，∠ACB＝90°，点D是边AB上一点，以BD为直径的⊙O与边AC相切于点E，连结DE并延长交BC的延长线于点F．[w&^ww~.*zz@step.com]
（1）求证：∠BDF=∠F；
（2）如果CF＝1，sinA＝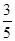
，求⊙O的半径．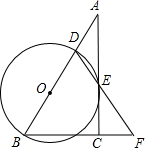
CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．
（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，
则BE_____CF；EF_____|BE﹣AF|（填“＞”，“＜”或“=”）；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件__________，使①中的两个结论仍然成立，并证明两个结论成立．
（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．
如图，在△ABC中，作∠ABC的平分线BD，交AC于D，作线段BD的垂直平分线EF，分别交AB于E，BC于F，垂足为O，连接DF．在所作图中，寻找一对全等三角形，并加以证明．（不写作法，保留作图痕迹）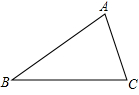
已知Rt△ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．
（1）当∠EDF绕D点旋转到DE⊥AC于E时（如图1），易证S△DEF+S△CEF= 
S△ABC；
（2）当∠EDF绕D点旋转到DE和AC不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，S△DEF、S△CEF、S△ABC又有怎样的数量关系？请写出你的猜想，不需证明．
求证：有一条直角边及斜边上的高对应相等的两个直角三角形全等．
如图，OB⊥AB，OC⊥AC，垂足为B，C，OB=OC，AO平分∠BAC吗？为什么？