在学习三角形中线的知识时,小明了解到:三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。进而,小明继续研究,过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分?他画出了如下示意图(如图1),得到了符合要求的直线AF.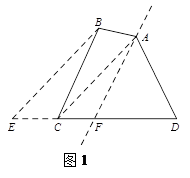
小明的作图步骤如下:
第一步:连结AC;
第二步:过点B作BE//AC交DC的延长线于点E;
第三步:取ED中点F,作直线AF;
则直线AF即为所求.
请参考小明思考问题的方法,解决问题:
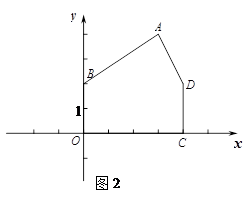
如图2,五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C(4,0),D(4,2).请你构造一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,并求出该直线的解析式.
从全校1200名学生中随机选取一部分学生进行调查,调查情况:
| A.上网时间≤1小时; | B.1小时<上网时间≤4小时; | C.4小时<上网时间≤7小时; | D.上网时间>7小时.统计结果制成了如图统计图: |
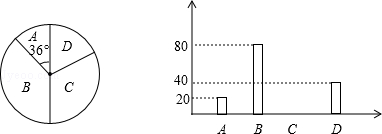
(1)参加调查的学生有 人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?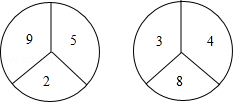
某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
| A型 |
B型 |
|
| 价格(万元/台) |
12 |
10 |
| 月污水处理能力(吨/月) |
200 |
160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC.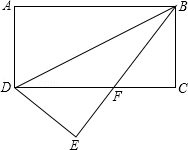
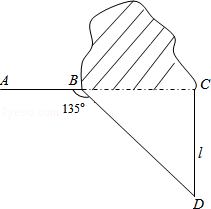
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(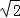 ≈1.414,精确到1米)
≈1.414,精确到1米)