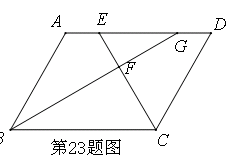
情境·观察:
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△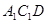 ,如图1所示,将△
,如图1所示,将△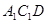 的顶点
的顶点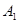 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A(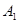 ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角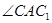 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。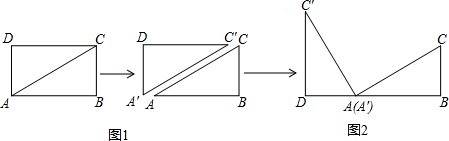
问题·探究:
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。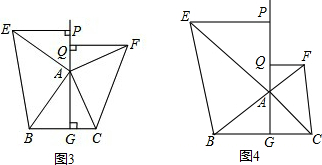
关系·拓展:
如图4,已知正方形ABCD,P为边BC上任意一点,连结AP,把AP绕点P顺时针方向旋转90°,点A对应点为点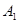 ,连接
,连接 ,求
,求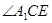 的度数。
的度数。
一次函数y=ax+b的图像分别与x轴,y轴交于点M,N,与反比例函数y= 的图像交于点A,B,过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E,过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F、D,AC与BD交于K,连接CD.
的图像交于点A,B,过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E,过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F、D,AC与BD交于K,连接CD.
若点A,B在反比例函数y=
 的图像的同一分支上,如图1,试证明:(1)AN=BM.
的图像的同一分支上,如图1,试证明:(1)AN=BM.若点A,B分别在反比例函数y=
 的图像的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论
的图像的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论
阅读材料:我们学过二次函数的图像的平移,如:将二次函数y=2x 的图像沿x轴向左平移3个单位长度得到函数y=2(x+3)
的图像沿x轴向左平移3个单位长度得到函数y=2(x+3) 的图像,再沿y轴向下平移1个单位长度,得到函数y=2(x+3)
的图像,再沿y轴向下平移1个单位长度,得到函数y=2(x+3) -1的图像.
-1的图像.
类似的,将一次函数y=2x的图像沿x轴向右平移1个单位长度可得到函数y=2(x-1)的图像,再沿y轴向上平移1个单位长度,得到函数y=2(x-1)+1的图像.
解决问题:将一次函数y= -x的图像沿x轴向右平移2个单位长度,再沿y轴向上平移3个单位长度,得到函数的图像;
将y=
 的图像沿y轴向上平移3个单位长度,得到函数的图像,再沿x轴向右平移1个单位长度,得到函数的图像;
的图像沿y轴向上平移3个单位长度,得到函数的图像,再沿x轴向右平移1个单位长度,得到函数的图像;函数y=
 的图像可由哪个反比例函数的图像经过怎样的变换得到?
的图像可由哪个反比例函数的图像经过怎样的变换得到?
某市海产品市场管理部门规划建造面积为2400平方米的集贸大棚,大棚内设A种类型和B种类型的店面共80间,每间A种类型的店面的平均面积为28平方米,月租费为400元;每间B种类型的店面的平均面积为20平方米,月租费为360元.全部店面的建造面积不低于大棚总面积的80%,又不能超过大棚总面积的85℅.试确定A种类型店面的数量的范围;
该大棚管理部门通过了解业主的租赁意向得知,A种类型店面的出租率为75%,B种类型店面的出租率为90%,为使店面的月租费最高,最高月租金是多少?
某风景管理区为提高游客到某景点的安全性,决定将到达该景点的步行台阶改善,把倾角由45°减至30°,已知原台阶坡面AB的长为5m(BC所在地面为水平面)。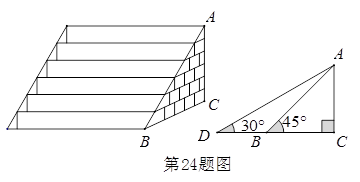
改善后的台阶坡面会加长多少?
改善后的台阶会多占多长一段水平地面?(结果精确到0.1)
如图,已知:□ABCD中,∠BCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G.求证:AE=DG.