已知 ,且
,且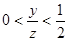 ,则
,则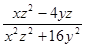 的最大值是 .
的最大值是 .
执行左图,输出的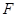 的值 .
的值 .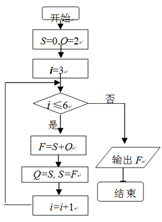
某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④27,54,81,128,135,162,189,216,243,270;
关于上述样本的下列结论中,可能为系统抽样的是 ;可能为分层抽样的是 .
为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互相不相同,则样本数据中的最大值为 .
口袋内装有一些大小相同的红球、白球和黒球,从中摸出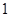 个球,摸出红球的概是
个球,摸出红球的概是 摸出白球的概率是
摸出白球的概率是 ,那么摸出黒球的概率是 .
,那么摸出黒球的概率是 .
若函数 在
在 上的最小值为
上的最小值为 ,则实数
,则实数 的值为 .
的值为 .