如图,设是圆上的动点,点是在轴上投影,为上一点,且.

(1)当在圆上运动时,求点的轨迹的方程;
(2)求过点且斜率为的直线被所截线段的长度.
(本小题满分12分)某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.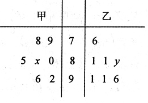
(1)求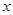 和
和 的值;
的值;
(2)计算甲组7位学生成绩的方差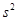 ;
;
(3)从成绩在90分以上的学生中随机取两名学生,求甲组至少有一
名学生的概率.
(本小题满分12分)如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且
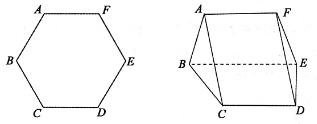
(1)证明:平面ABEF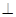 平面BCDE;
平面BCDE;
(2)求三棱锥 的体积
的体积
(本小题满分12分)已知函数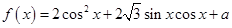 ,且当
,且当 时,
时, 的最小值为2,
的最小值为2,
(1)求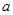 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(2)先将函数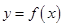 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的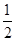 ,再将所得的图象向右平移
,再将所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求方程
的图象,求方程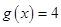 在区间
在区间 上所有根之和.
上所有根之和.
(本小题满分14分)已知焦点在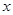 轴上的椭圆
轴上的椭圆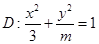 的离心率为
的离心率为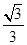 ,
,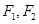 分别为左右焦点,过点
分别为左右焦点,过点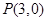 作直线交椭圆
作直线交椭圆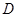 于
于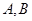 (
(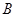 在
在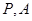 两点之间)两点,且
两点之间)两点,且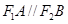 ,
,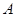 关于原点
关于原点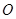 的对称点为
的对称点为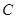 .
.
(1)求椭圆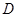 的方程;
的方程;
(2)求直线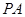 的方程;
的方程;
(3)过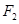 任作一直线交过
任作一直线交过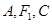 三点的圆于
三点的圆于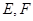 两点,求
两点,求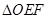 面积的取值范围.
面积的取值范围.
(本小题满分13分)已知函数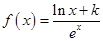 (其中
(其中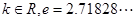 是自然对数的底数),
是自然对数的底数),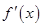 为
为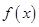 导函数。
导函数。
(1)当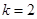 时,其曲线
时,其曲线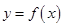 在点
在点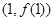 处的切线方程;
处的切线方程;
(2)若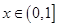 时,
时,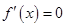 都有解,求
都有解,求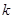 的取值范围;
的取值范围;
(3)若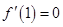 ,试证明:对任意
,试证明:对任意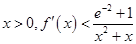 恒成立.
恒成立.