设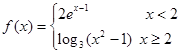 ,则不等式
,则不等式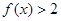 的解集为()
的解集为()
A.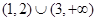 |
B.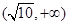 |
C.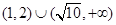 |
D.(1,2) |
如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,不一定成立的为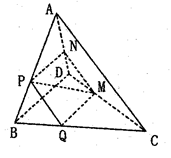
| A.AC⊥BE | B.AC//截面PQMN |
| C.异面直线PM与BD所成的角为45° | D.AC=BD |
一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是()
A. 海里 B.
海里 B. 海里 C.
海里 C.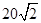 海里 D.
海里 D. 海里
海里
设函数 为奇函数,
为奇函数,
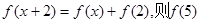 =()
=()
| A.0 | B.1 | C.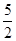 |
D.5 |
如图是一个算法的程序框图,若该程序输出的结果为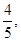
则判断框中应填入的条件是()
| A.T>4 | B.T<4 | C.T>3 | D.T<3 |