
小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以为起点,再从,(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为。若就参加学校合唱团,否则就参加学校排球队。
(1)求小波参加学校合唱团的概率;
(2)求的分布列和数学期望.
在一段时间内,某种商品价格 (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
价格 |
1.4 |
1.6 |
1.8 |
2 |
2.2 |
需求量 |
12 |
10 |
7 |
5 |
3 |
(1)进行相关性检验;
(2)如果 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01 )
)
参考公式及数据: ,
, ,
,
相关性检验的临界值表:
| n-2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 小概率0.01 |
1.000 |
0.990 |
0.959 |
0.917 |
0.874 |
0.834 |
0.798 |
0.765 |
0.735 |
0.708 |
在△ABC中, ,记
,记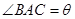 ,△ABC的面积为
,△ABC的面积为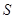 ,且满足
,且满足 .
.
(1)求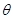 的取值范围;
的取值范围;
(2)求函数 的最大值和最小值.
的最大值和最小值.
已知函数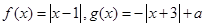

(I) 解关于 的不等式
的不等式  ;
;
(II)若函数 的图象恒在函数
的图象恒在函数 的上方,求实数
的上方,求实数 的取值范围。
的取值范围。
以直角坐标系的原点O为极点, 轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,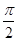 ),若直线
),若直线 过点P,且倾斜角为
过点P,且倾斜角为 ,圆C以M为圆心,4为半径。
,圆C以M为圆心,4为半径。
(I)求直线 的参数方程和圆C的极坐标方程;
的参数方程和圆C的极坐标方程;
(II)试判定直线 与圆C的位置关系。
与圆C的位置关系。
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,
垂是为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点。
(I)求证:∠PFE=∠PAB;
(II)求证:CD2=CF·CP.