已知点 是抛物线
是抛物线 上不同的两点,点
上不同的两点,点 在抛物线
在抛物线 的准线
的准线 上,且焦点
上,且焦点 到直线
到直线 的距离为
的距离为 .
.
(I)求抛物线 的方程;
的方程;
(2)现给出以下三个论断:①直线 过焦点
过焦点 ;②直线
;②直线 过原点
过原点 ;③直线
;③直线 平行
平行 轴.
轴.
请你以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题,并加以证明.
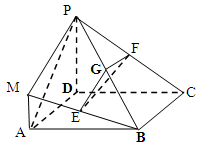
在如图所示的几何体中,四边形 是正方形,
是正方形,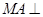 平面
平面 ,
, ,
, 分别为
分别为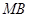 ,
,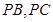 的中点,且
的中点,且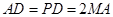 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求三棱锥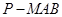 与四棱锥
与四棱锥 的体积之比.
的体积之比.
南充市某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为 ,
, ,经测量
,经测量 米,
米, 米,
米, 米,
米,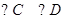 .
.
(Ⅰ)求 的长度;
的长度;
(Ⅱ)若环境标志的底座每平方米造价为5000元,不考虑其他因素,小李、小王谁的设计使建造费用最低(请说明理由)?最低造价为多少?(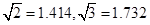 )
)
已知 是正数列组成的数列,
是正数列组成的数列,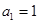 ,且点
,且点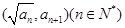 在函数
在函数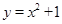 的图像上,
的图像上,
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若数列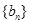 满足
满足 ,
, ,求证:
,求证: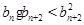 .
.
设函数f(x)=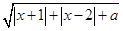 .
.
(Ⅰ)当a=-5时,求函数f(x)的定义域;
(II)若函数f(x)的定义域为R,试求a的取值范围.
已知曲线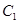 的参数方程为
的参数方程为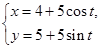 (
(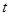 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线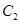 的极坐标方程为
的极坐标方程为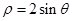 .
.
(Ⅰ)把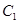 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(Ⅱ)求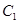 与
与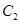 交点的极坐标(
交点的极坐标( ).
).