如图所示，倾角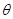
=30°。的光滑斜面MN底端固定一轻弹簧，轻弹簧的上端与滑块A固定连接，弹簧劲度系数k-100N/m，A静止且与距斜面顶端N点相距x=0．10m。另一小滑块B在N点以初速度
沿斜面向下运动，A、B碰撞后具有相同速度但不粘连。B与A分离后，B恰水平进入停放在光滑水平地面上的小车最左端，小车右端与墙壁足够远，小车上表面与半圆轨道最低点P的切线相平，小车与墙壁碰撞时即被粘在墙壁上。已知水平地面和半圆轨道面均光滑，滑块A、B可视为质点且质量均为m=2kg，被A压缩时弹簧存储的弹性势能Ep=0．5J，小车质量M=lkg、长L=l．0m，滑块B与小车上表面间的动摩擦因数
=0．2，g取l0m/s2。求：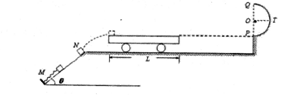
（I）滑块B与A碰撞结束瞬间的速度；
（2）小车与墙壁碰撞前瞬间的速度；
（3）为使滑块B能沿圆轨道运动而不脱离圆轨道，对轨道半径R有何要求？
弹簧振子以O点为平衡位置在B、C两点间做简谐运动，B、C相距20 cm，某时刻振子处于B点，经0.5 s振子首次到达C点.求：
(1)振子的振幅、周期；
(2)振子在5 s内通过的路程和5 s末相对平衡位置位移的大小.
如图所示，地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动。地球的轨道半径为R，运转周期为T，地球和太阳中心的连线与地球和行星中心的连线所夹的角叫地球对该行星的观察视角（简称视角）。已知该行星的最大视角为
，当行星处于最大视角时是地球上的天文爱好者观察该行星的最佳时期。某时刻该行星恰好处于最佳观察期，且行星的位置超前于地球。求：
（1）行星绕太阳运转的周期
（2）该行星下一次处于最佳观察期至少经历的时间。
如图所示，在匀速转动的圆盘上，沿半径方向放置以细线相连的质量均为m的A、B两个小物块，A离轴心r1＝20 cm，B离轴心r2＝30 cm，A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍．求：
(1)若细线上没有张力，圆盘转动的角速度ω应满足什么条件？
(2)欲使A、B与盘面间不发生相对滑动，则盘转动的最大角速度多大？
(3)当圆盘转速达到A、B刚好不滑动时，烧断细绳，则A、B将怎样运动？(g取10 m/s2)
如图所示，长度为l的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小可以忽略）。、
（1）在水平拉力F的作用下，轻绳与竖直方向的夹角为
，小球保持静止，画出此时小球的受力图，并求力F的大小。
（2）由图示位置无初速度释放小球，求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。
如图所示，巡查员站立于一空的贮液池边，检查池角出液口的安全情况．已知池宽为L，照明灯到池底的距离为H，若保持照明光束方向不变，向贮液池中注入某种液体，当液面高为
时，池底的光斑距离出液口
.
(1)试求当液面高为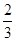
H时，池底的光斑到出液口的距离x.
(2)控制出液口缓慢地排出液体，使液面以vh的速率匀速下降，试求池底的光斑移动的速率vx.