如图所示为一个均匀透明介质球,球心位于O点,半径为R.一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H= R.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )
R.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )
A.介质球的折射率为 |
B.光束从C点射入到从E点射出所经历的总时间为 |
| C.射入球体内的光线有可能发生全反射 |
| D.若介质球的折射率增大,则该出射光线仍与入射光线平行 |
下列说法正确的是
| A.某种液体的饱和蒸气压与温度有关 |
| B.物体内所有分子热运动动能的总和就是物体的内能 |
| C.气体的温度升高,每个分子的动能都增大 |
| D.不是所有晶体都具有各向异性的特点 |
以下说法正确的是
| A.当分子间距离增大时,分子间作用力减小,分子势能增大 |
| B.某固体物质的摩尔质量为M,密度为ρ,阿伏加德罗常数为NA,则该物质的分子的体积为V0 = M/(ρNA) |
| C.液晶既具有液体的流动性,又具有单晶体的光学各向异性的特点 |
| D.自然界发生的一切过程能量都是守恒的,符合能量守恒定律的宏观过程都能自然发生 |
如题21图所示,水平向左的匀强电场中,长为L的绝缘细线一端固定于O点,另一端系一质量为m、电荷量为q的可视为质点的带正电小球.将小球拉到使细线水平伸直的A点,无初速释放小球,小球沿圆弧到达最低位置B时速度恰好为零,重力加速度为g以下说法正确的是
A.匀强电场场强大小为E= |
| B.小球在B位置时加速度为零 |
C.小球运动过程中的最大速率为v= |
| D.若将小球拉到使细线水平伸直的C点,无初速释放小球后,小球必能回到C点 |
如题20图所示为重庆某中学教学区供电示意图,供电部门通过理想变压器原线圈A、B端送电,虚线框内表示教学区内各教室的照明电路.已知变压器副线圈C、D端距教学区输入端E、F距离较远,之间输电线电阻不能忽略,设定A、B端输入电压一定,则以下说法正确的是
A.如果教学区同时使用的电灯减少,A、B端输入电功率仍不变
B.C D端电压一定为220V
C.EF端电压一定为220V
D.教学区内同时使用的电灯越多,EF端输入电压越低
如题19图所示,倾角为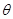 的光滑绝缘斜面上放置质量分别为m、2m相距L可视为点电荷的带电小球A、B将小球A、B同时无初速释放,已知释放瞬时小球A的加速度为零,经过一段时间,小球A、B间的距离为x时,两者的加速度大小分别为aA、aB大小关系为aB -1.5aA,重力加速度为g,则以下说法
的光滑绝缘斜面上放置质量分别为m、2m相距L可视为点电荷的带电小球A、B将小球A、B同时无初速释放,已知释放瞬时小球A的加速度为零,经过一段时间,小球A、B间的距离为x时,两者的加速度大小分别为aA、aB大小关系为aB -1.5aA,重力加速度为g,则以下说法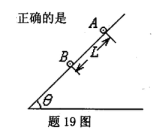
A.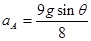
B.x= 2L
C.运动过程中,小球A、B系统机械能守恒
D.释放瞬时小球B的加速度大小为gsin