如图是一组滑轮装置,绳子都处于竖直状态,不计绳子和滑轮质量及一切阻力,悬挂的两物体质量分别为 m1=m,m2=4m,m1下端通过劲度系数为k的轻质弹簧与地面相连(重力加速度为g,轻质弹簧始终处于弹性限度之内)求: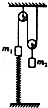
(1)系统处于静止时弹簧的形变量;
(2)用手托住m2且让m1静止在弹簧上,绳子绷直但无拉力,放手之后两物体的运动发生在同一竖直平面内,求m2运动的最大速度.
如图所示,摩托车运动员做飞越壕沟的特技表演,摩托车以初速度V 0冲上顶部水平的高台,高台后面是一条宽L=10m的壕沟,若摩托车冲上高台过程中以恒定功率P=1.8kW行驶,经历时间t=5s,到达高台顶部时立即关闭发动机,摩托车在水平的高台上做匀速直线运动一段距离后飞离高台。已知人和车的总质量m=180kg(可视为质点),平台高h=5m,忽略空气阻力和摩擦阻力。取g=10m/s 2。问:(1)V 0至少应多大?(2)假定摩托车落地速度大小超过Vm =30m/s时会对运动员造成危险,则摩托车飞离高台时的最大速度Vm′应为多少?
从高H处由静止释放一球,它在运动过程中受大小不变的阻力f。若小球质量为m,碰地过程中无能量损失,求(1)小球第一次碰地后反弹的高度是多少?(2)小球从释放直至停止弹跳的总路程为多少?
游乐场中的翻腾过山车从某一高度滑下后,进入竖直面上的圆轨道运动,当过山车经过圆轨道顶端时,也不会掉下来,是一种惊险刺激的运动,其物理模型如图所示。设过山车的质量为m,过山车自A点无初速沿轨道滑下,后进入圆轨道,圆轨道的半径为R,A点的高度h=4R,不计空气阻力和摩擦阻力,求过山车到圆轨道最高点B时的速度大小。
额定功率为80KW的汽车, 汽车的质量m=2×10 ㎏,在平直公路上行驶的最大速度为20m/s,如果汽车从静止开始做匀加速直线运动,加速度大小为2 m/s
㎏,在平直公路上行驶的最大速度为20m/s,如果汽车从静止开始做匀加速直线运动,加速度大小为2 m/s ,运动过程中阻力不变,求:(1)汽车所受的恒定阻力。 (2)3s末汽车的瞬时功率。 (3)经过多长时间汽车功率达到额定功率。
,运动过程中阻力不变,求:(1)汽车所受的恒定阻力。 (2)3s末汽车的瞬时功率。 (3)经过多长时间汽车功率达到额定功率。
把一小球从离地面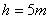 处,以
处,以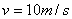 的初速度水平抛出,不计空气阻力, (g=10m/s2)。求:(1)小球在空中飞行的时间;(2)小球落地点离抛出点的水平距离。
的初速度水平抛出,不计空气阻力, (g=10m/s2)。求:(1)小球在空中飞行的时间;(2)小球落地点离抛出点的水平距离。