如图所示，一个折射率为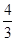
的三棱镜的截面为等腰直角△ABC，∠A为直角．此截面所在平面内的一束光线沿与AB边成θ角（θ＜90°）的方向入射到AB边的中点P处，若要光线进入三棱镜后能射到AC边上且能在AC面上发生全反射，则cosθ应满足什么条件？
某课外小组经长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R1，周期为T1，已知万有引力常为G。求：
⑴行星的质量；
⑵若行星的半径为R，行星的第一宇宙速度；
⑶通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R2，周期为T2，试估算靠近行星周围众多卫星的总质量(提示:研究很远的卫星可把其他卫星和行星整体作为中心天体)。
我国“神舟”九号宇宙飞船已经发射成功，当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图，如图所示，它记录了“神舟”六号飞船在地球表面垂直投影的位置变化；图中表示在一段时间内飞船绕地球圆周飞行四圈，依次飞经中国和太平洋地区的四次轨迹①、②、③、④，图中分别标出了各地点的经纬度（如：在轨迹①通过赤道时的经度为西经157.5°，绕行一圈后轨迹②再次经过赤道时经度为180°……），若地球半径为R=6400km，地球表面处的重力加速度g=10m/s2，从图中的信息计算“神舟”九号宇宙飞船的
（1）运行周期 （2）飞船离地面的高度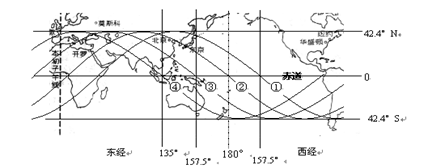
在用高级沥青铺设的高速公路上，汽车的设计时速是108km/h。汽车在这种路面上行驶时，它的轮胎与地面的最大静摩擦力等于车重的0.6倍。
（1）如果汽车在这种高速路的水平弯道上拐弯，假设弯道的路面是水平的，其弯道的最小半径是多少？
（2）如果高速路上设计了圆弧拱桥做立交桥，要使汽车能够以设计时速安全通过圆弧拱桥，这个圆弧拱桥的半径至少是多少？（取g=10m/s2）
飞机在2 km的高空以100m/s的速度水平匀速飞行,相隔1ｓ,先后从飞机上掉下A、B两物体,不计空气阻力,求两物体在空中的最大距离是多少?（g＝10 m/s2）
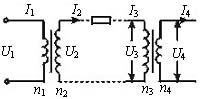
如图所示，发电机输出功率P1="100" kW，输出电压U1="250" V，用户需要的电压U4="220" V，输电线总电阻为10 Ω.若输电线中因发热而损失的功率为输送功率的4%，试求：
（1）发电机的输送电流I1是多少？
（2）在输电线路中设置的升、降压变压器原副线圈的匝数比n1：n2.
（3）用户得到的电功率P4是多少？