如图所示，倾角450高h的固定斜面。右边有一高3h/2的平台，平台顶部左边水平，上面有一质量为M的静止小球B，右边有一半径为h的1/4圆弧。质量为m的小球A从斜面底端以某一初速度沿斜面上滑，从斜面最高点飞出后恰好沿水平方向滑上平台，与B发生弹性碰撞，碰后B从圆弧上的某点离开圆弧。所有接触面均光滑，A、B均可视为质点，重力加速度为g。
（1）求斜面与平台间的水平距离S和A的初速度v0；
（2）若M=2m，求碰后B的速度；
（3）若B的质量M可以从小到大取不同值，碰后B从圆弧上不同位置脱离圆弧，该位置与圆心的连线和竖直方向的夹角为α。求cosα的取值范围。
如图所示，一足够长的固定斜面倾角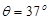
，两物块A、B的质量分别为
、
分别为1kg和4kg，它们与斜面之间的动摩擦因数均为
。两物块之间的轻绳长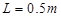
，轻绳承受的最大张力T＝12N，作用于B上沿斜面向上的力F逐渐增大，使A、B一起由静止开始沿斜面向上运动，
。（
，
）
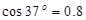⑴某一时刻轻绳被拉断，求此时外力F的大小；
⑵若轻绳拉断前瞬间A、B的速度为3m/s，绳断后保持外力F不变，求当A运动到最高点时，A、B之间的距离。
如图所示，倾角为θ的斜面处于竖直向下的匀强电场中，在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球，小球在电场中受到的电场力与小球所受的重力相等。设斜面足够长，地球表面重力加速度为g，不计空气的阻力，求：
（1）小球落到斜面所需时间t；
（2）小球从水平抛出至落到斜面的过程中电势能的变化量ΔE。
如图所示，轻弹簧的两端与质量均为2m的B、C两物块固定连接，静止在光滑水平面上，物块C紧靠挡板但不粘连．另一质量为m的小物块A以速度v0从右向左与B发生弹性正碰，碰撞时间极短可忽略不计．(所有过程都在弹簧弹性限度范围内)求：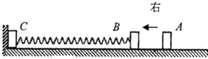
(1)A、B碰后瞬间各自的速度；
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比．
在折射率为n，厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以入射角θ入射到玻璃板上表面，经过玻璃板后从下表面射出，如图所示。若沿此光线传播的光从光源 S 到玻璃板上表面的传播时间与在玻璃板中传播时间相等，点光源S到玻璃板上表面的垂直距离l应是多少？
如图所示，内壁光滑的气缸竖直放置，在距气缸底部l=36cm处有一与气缸固定连接的卡环，活塞与气缸底部之间封闭了一定质量的气体。当气体的温度 T1=300K、大气压强 P0=1.0×105Pa时，活塞与气缸底部之间的距离l0=30cm，已知活塞面积为50cm2，不计活塞的质量和厚度。现对缸内气体加热，使活塞缓慢上升，当温度上升至T2=540K时，求：
①封闭气体此时的压强；②该过程中气体对外做的功。