如图所示,质量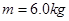 的滑块(可视为质点),在F=60N的水平拉力作用下从A点由静止开始运动,一段时间后撤去拉力F,当滑块由平台边缘B点飞出后,恰能从水平地面上的C点沿切线方向落入竖直圆弧轨道CDE,并从轨道边缘E点竖直向上飞出,经过0.4 s后落回E点。已知AB间的距离L="2.3" m,滑块与平台间的动摩擦因数
的滑块(可视为质点),在F=60N的水平拉力作用下从A点由静止开始运动,一段时间后撤去拉力F,当滑块由平台边缘B点飞出后,恰能从水平地面上的C点沿切线方向落入竖直圆弧轨道CDE,并从轨道边缘E点竖直向上飞出,经过0.4 s后落回E点。已知AB间的距离L="2.3" m,滑块与平台间的动摩擦因数 ,平台离地高度
,平台离地高度 ,B、C两点间水平距离s="1.2" m,圆弧轨道半径R=1.0m。重力加速度g取10 m/s2,不计空气阻力。求:
,B、C两点间水平距离s="1.2" m,圆弧轨道半径R=1.0m。重力加速度g取10 m/s2,不计空气阻力。求: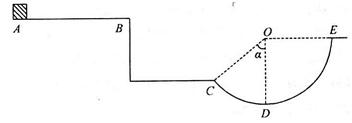
(1)滑块运动到B点时的速度大小;
(2)滑块在平台上运动时受水平拉力F作用的时间;
(3)分析滑块能否再次经过C点。
直流发电机ε="250" V,r="3" Ω,两条输电线电阻R1=R2="1" Ω,并联的电热器组中装有50只完全相同的电热器,每只电热器的额定电压为200 V,额定功率为1 000 W,其它电阻不计,并且不计电热器电阻随温度的变化,求:
(1) 接通几只电热器时,实际使用的电热器都能正常工作?
(2) 接通几只电热器时,发电机的输出功率最大?
(3) 接通几只电热器时,电热器组加热物体最快?
(4) 接通几只电热器时,电阻R1和R2上消耗的功率最大?
(5) 接通几只电热器时,实际使用的每只电热器中的电流最大?
某电炉在额定电压下的电功率为P0=400W,电源在不接负载时的路端电压与电炉的额定电压相同.当把电炉接到该电源时,电炉实际消耗的功率为P1=324W.若将两个这样的电炉并联接入该电源,那么两个电炉实际消耗的总功率P2为多少?
如图所示为一由双刀双掷电键S、两节干电池(每节干电池的电动势ε=1.5V,内阻r=1Ω)和一个小灯泡(额定电压为2.5V,额定电流为0.15A)组成的电路,那么: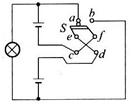
(1)当触刀掷向a、b时(a和e、d接通,b和f、c接通),两个电池是怎样连接的?小灯泡消耗的功率是多少?
(2)当触刀掷向c、d时,两个电池是怎样连接的?小灯泡消耗的功率是多少?
如图所示,变阻器R2的最大电阻是10 Ω,R3=5 Ω,电源的内电阻r=1 Ω,当电键S闭合,变阻器的滑片在中点位置时,电源的总功率为16 W,电源的输出功率为12 W.此时电灯R1正常发光,求:
(1)电灯阻值R1是多少?(设R1阻值恒不变)
(2)当电键S断开时,要使电灯正常工作,应使变阻器的电阻改变多少?
如图所示,电阻R3=4 Ω,电表为理想表.开始时R1、R2、R3中都有电流通过,电压表示数为2 V,电流表示数为0.75 A.后来三个电阻中有一个发生断路,使电压表示数变为3.2 V,电流表示数变为0.8 A.
(1)哪个电阻断路?
(2)求电阻R1、R2的阻值各为多少?
(3)电源电动势和内阻各为多少?