汽车从A地出发到B地，以初速度
加速度
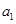从A地出发后做匀加速直线运动，到达中点时速度为
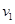然后改以加速度
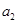继续匀加速直线运动，到达B地时速度大小为
，已知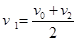
，则前半程和后半程的加速度大小关系为（ ）
A． |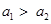
B． |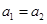
C． |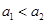
D．无法确定 |
矩形线圈在匀强磁场中匀速转动，从中性面开始转动180°的过程中，平均感应电动势和最大感应电动势之比为( )
| A．π/2 | B．2/π | C．2π | D．π |
交变电压的瞬时值为u＝Umsin100πt(V)，当t＝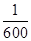
s时，u＝52 V，则从电压表上看到的读数为( )
| A．2 V | B．52 V | C．10√2 V | D．10 V |
某交流电电压为u＝10√2sin314t(V)，则( )
| A．击穿电压为10 V的电容器能直接接在此电源上 |
| B．把电磁打点计时器接在此电源上，打点周期为0.01 s |
| C．把额定电压为10 V的小灯泡直接接在此电源上，小灯泡将被烧坏 |
| D．把额定电压为10 V的小灯泡直接接在此电源上，小灯泡能正常发光 |
下列关于交流电的说法中正确的是( )
| A．交流电器设备上所标的电压和电流值是交流电的峰值 |
| B．用交流电流表和电压表测定的读数值是交流电的瞬时值 |
| C．给定的交流数值，在没有特别说明的情况下是指有效值 |
| D．跟交变电流有相同的热效应的直流电的数值是交流电的平均值 |
在O点有一波源，t＝0时刻开始向上振动，形成向右传播的一列横波．t1＝4 s时，距离O点为3 m的A点第一次达到波峰；t2＝7 s时，距离O点为4 m的B点第一次达到波谷．则以下说法正确的是( )
| A．该横波的波长为2 m |
| B．该横波的周期为4 s |
| C．该横波的波速为1 m/s |
| D．距离O点为5 m的质点第一次开始向上振动的时刻为6 s末 |