给出30个数：1，2,4,7，……其规律是：第1个数是1；第2个数比第1个数大1；第3个数比第2个数大2；第4个数比第3个数大3；……以此类推，要计算这30个数的和，现已给出了该问题的程序框图如图所示，那么框图中判断框①处和执行框②处应分别填入（ ）
A． |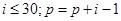
B． |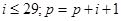
C． |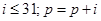
D． |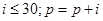
已知函数，
’若
在(0,
)上单调递减,则实数a的取值范围为
A．(0, ) |
B．(0, ] |
C．[ ) |
D．( ,1) |
在正方体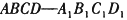
中，M为
的中
点,0为底面ABCD的中心,P为棱
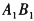的中点,则直线OP与直线AM所成的角是
A． |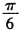
B． |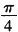
C． |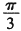
D． |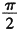
将4名志愿者分配到3所不同的学校进行学生课外活动内容调查,每个学校至少分配一名志愿者的方案种数为
| A．24 | B．36 | C．72 | D．144 |
某学校对高二年级一次考试进行抽样分析.右图是根据抽样分析后的考试成绩绘制的频率分布直方图,其中抽样成绩的范围是[96,106]，样本数据分组为[%，兇），[98,100)，[100，102)，[102,104),[ 104,106].已知样本中成绩小于100分的人数是36，则样本中成绩大于或等于98分且小于
104分的人数
是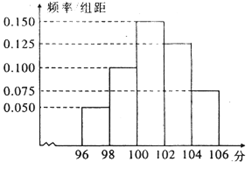
| A．90 | B．75 | C．60 | D．45 |
若变量x,y满足约束条件
则目标函数Z==x+2y的取值范围是
| A．[2,6] | B．[2,5] | C．[3,6] | D．[3,5] |