如图,椭圆 的长轴长为
的长轴长为 ,点
,点 、
、 、
、 为椭圆上的三个点,
为椭圆上的三个点, 为椭圆的右端点,
为椭圆的右端点, 过中心
过中心 ,且
,且 ,
, .
.
(1)求椭圆的标准方程;
(2)设 、
、 是椭圆上位于直线
是椭圆上位于直线 同侧的两个动点(异于
同侧的两个动点(异于 、
、 ),且满足
),且满足 ,试讨论直线
,试讨论直线 与直线
与直线 斜率之间的关系,并求证直线
斜率之间的关系,并求证直线 的斜率为定值.
的斜率为定值.
椭圆 :
:
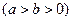 的两个焦点为
的两个焦点为 、
、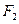 ,点
,点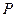 在椭圆
在椭圆 上,且
上,且 ,
, ,
, .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线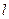 过圆
过圆 的圆心
的圆心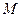 ,交椭圆
,交椭圆 于
于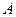 、
、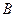 两点,且
两点,且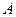 、
、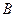 关于点
关于点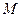 对称,求直线
对称,求直线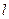 的方程.
的方程.
设函数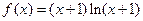 ,若对所有的
,若对所有的 ,都有
,都有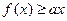 成立,求实数
成立,求实数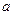 的取值范围.
的取值范围.
如图,在四棱锥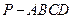 中,底面
中,底面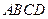 为矩形,侧棱
为矩形,侧棱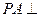 底面
底面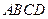 ,
,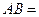
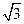 ,
, ,
,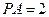 ,
,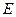 为
为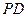 的中点.
的中点.
(Ⅰ)求直线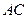 与
与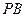 所成角的余弦值;
所成角的余弦值;
(Ⅱ)在侧面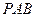 内找一点
内找一点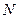 ,使
,使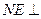 面
面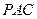 ,并求出
,并求出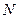 点到
点到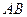 和
和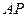 的距离.
的距离.
已知直线l的参数方程为 ,曲线C的参数方程为
,曲线C的参数方程为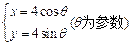 .
.
(Ⅰ)将曲线C的参数方程转化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,试求线段AB的长
有红蓝两粒质地均匀的正方体骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜。
(Ⅰ)分别求出两只骰子投掷所得点数的分布列及期望;
(Ⅱ)求投掷蓝色骰子者获胜的概率是多少?