一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行)。下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
(1)写出渔船离港口的距离S和它离开港口的时间t的函数关系式;
(2)在渔船返航途中,什么时间范围内两船间距离不超过30海里?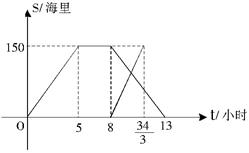
如图,已知△ABC的三个顶点的坐标分别为A(﹣6,0)、B(﹣2,3)、C(﹣1,0).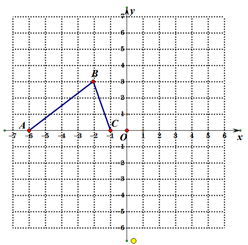
(1)请直接写出与点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
关于 的一元二次方程
的一元二次方程 有实数解.
有实数解.
(1)求k的取值范围;
(2)如果 且k为整数,求k的值.
且k为整数,求k的值.
解方程
(1) ;
;
(2)3(x-2)2=x(x-2)
如图,直线 与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线
与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线 与x轴的另一个交点为A,顶点为P.
与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.