汤姆孙测定电子比荷的实验装置如图甲所示。从阴极K发出的电子束经加速后,以相同速度沿水平中轴线射入极板D1、D2区域,射出后打在光屏上形成光点。在极板D1、D2区域内,若不加电场和磁场,电子将打在P1点;若只加偏转电压U,电子将打在P2点;若同时加上偏转电压U和一个方向垂直于纸面向外、磁感应强度大小为B的匀强磁场(图中未画出),电子又将打在P1点。已知极板长度为L,极板间距为d。忽略电子的重力及电子间的相互作用。

(1)求电子射人极板D1、D2区域时的速度大小;
(2)打在P2点的电子,相当于从D1、D2中轴线的中点O’射出,如图乙中的O’ P2所示,已知 试推导出电子比荷
试推导出电子比荷 的表达式;
的表达式;
(3)若两极板间只加题中所述的匀强磁场,电子在极板间的轨迹为一段圆弧,射出后打在P3点。测得圆弧半径为2L、P3与P1间距也为2L,求图乙中P1与P2点的间距a。
如图所示,水平放置的两块平行金属板长l =5cm,两板间距d=1cm,两板间电压为U=90V,且上板带正电,一个电子沿水平方向以速度v0=2.0×107m/s,从两板中央射入,求: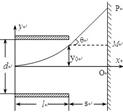
(1)电子偏离金属板的侧位移y0是多少?
(2)电子飞出电场时的速度是多少?
(3)电子离开电场后,打在屏上的P点,若s=10cm,求OP的长。
如图所示,电源的电动势E=110V,电阻R1=21Ω,电动机绕组的电阻R0=0.5Ω,电键S1始终闭合。当电键S2断开时,电阻R1的电功率是525W;当电键S2闭合时,电阻R1的电功率是336W,求: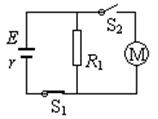
(1)电源的内电阻; (2)当电键S2闭合时流过电源的电流和电动机的输出功率。
如图,R1=14Ω,R2=9Ω,当开关处于位置1时,电流表读数I1=0.2A;当开关处于位置2时,电流表读数I2=0.3A,求电源的电动势E和内电阻r。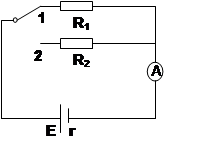
为了安全,公路上行驶的汽车间应保持必要的距离。某市规定,车辆在市区内行驶的速度不得超过40km/h。有一辆车发现前面25m处发生交通事故紧急刹车,紧急刹车产生的最大加速度为5m/s2,反应时间为t=0.5s。经测量,路面刹车痕迹为S=14.4m。该汽车是否违章驾驶?是否会有安全问题?
如图所示,重物A质量为mA=5kg,重物B质量为mB=2kg,A与桌面间的最大静摩擦力的fm=10N,为使系统处于静止状态,试求拉力F的大小。(g取10m/s2)