.图为一种节能系统：斜面轨道倾角为30°，质量为M的木箱与轨-优题课

.图为一种节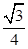能系统：斜面轨道倾角为30°，质量为M的木箱与轨道的动摩擦因数为。木箱在轨道顶端时，自动装货装置将质量为m的货物装入木箱，然后木箱载着货物沿轨道无初速下滑，轻弹簧被压缩至最短时，自动卸货装置立刻将货物卸下，之后木箱恰好被弹回到轨道顶端，再重复上述过程。下列判断正确的是（）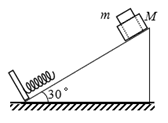

A．下滑过程中木箱克服轨道摩擦力做的总功等于货物减少的重力势能

B．下滑过程中木箱始终做匀加速直线运动

C．m = 6M

D．M = 6m

科目物理题型选择题难度中等

如图，一粗糙斜面固定在地面上，斜面顶端装有一光滑定滑轮。一细绳跨过滑轮，其一端悬挂物块N。另一端与斜面上的物块M相连，系统处于静止状态。现用水平向左的拉力缓慢拉动N，直至悬挂N的细绳与竖直方向成45°。已知M始终保持静止，则在此过程中（）

A．水平拉力的大小可能保持不变

B．M所受细绳的拉力大小一定一直增加

C．M所受斜面的摩擦力大小一定一直增加

D．M所受斜面的摩擦力大小可能先减小后增加

如图，篮球架下的运动员原地垂直起跳扣篮，离地后重心上升的最大高度为H。上升第一个 $\frac{H}{4}$ 所用的时间为 $t_{1}$ ，第四个 $\frac{H}{4}$ 所用的时间为 $t_{2}$ 。不计空气阻力，则 $\frac{t_{2}}{t_{1}}$ 满足（）

A. $1 < \frac{t_{2}}{t_{1}} < 2$ B. $2 < \frac{t_{2}}{t_{1}} < 3$ C. $3 < \frac{t_{2}}{t_{1}} < 4$ D. $4 < \frac{t_{2}}{t_{1}} < 5$

如图，等边三角形线框 $LMN$ 由三根相同的导体棒连接而成，固定于匀强磁场中，线框平面与磁感应强度方向垂直，线框顶点 $M 、 N$ 与直流电源两端相接，已如导体棒 $MN$ 受到的安培力大小为F，则线框 $LMN$ 受到的安培力的大小为( )

A. $2 F$ B. $1.5 F$ C. $0.5 F$ D. $0$

最近，我国为"长征九号"研制的大推力新型火箭发动机联试成功，这标志着我国重型运载火箭的研发取得突破性进展。若某次实验中该发动机向后喷射的气体速度约为 $3 km / s$ ，产生的推力约为 $4.8 \times 10^{6} N$ ，则它在 $1 s$ 时间内喷射的气体质量约为（）

A． $1.6 \times 102 kg$ B． $1.6 \times 103 kg$ C． $1.6 \times 105 kg$ D． $1.6 \times 106 kg$

如图，空间存在一方向水平向右的匀强磁场，两个带电小球 $P$ 和 $Q$ 用相同的绝缘细绳悬挂在水平天花板下，两细绳都恰好与天花板垂直，则（）

A． $P$ 和 $Q$ 都带正电荷

B． $P$ 和 $Q$ 都带负电荷

C． $P$ 带正电荷， $Q$ 带负电荷

D． $P$ 带负电荷， $Q$ 带正电荷