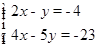小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
如图,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.

(1)如图1,试说明 ;
;
(2)如图2,若AB=AC,BE=12,CF=5,求△DEF的面积.
爸爸想送Mike一个书包和随身听作为新年礼物.在家乐福、人民商场都发现同款的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元,
(1)求随身听和书包单价各是多少元。
(2)新年来临赶上商家促销,人民商场所有商品打八折销售,家乐福全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家购买看中的这两样物品,你能帮助他选择在哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
甲、乙两位同学本学年每个单元的测验成绩如下(单位:分):
甲:98,100,100,90,96,91,89,99,100,100,93
乙:98,99,96,94,95,92,92,98,96,99,97
(1)、他们的平均成绩分别是多少?
(2)、甲、乙的11次单元测验成绩的标准差分别是多少?
(3)、这两位同学的成绩各有什么特点?
(4)、现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么?
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△ ,使它与△ABC 关于x轴对称,并写出△
,使它与△ABC 关于x轴对称,并写出△ 三顶点的坐标.
三顶点的坐标.
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△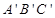 内部的对应点M'的坐标.
内部的对应点M'的坐标.
解方程组(1)、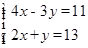 (2)、
(2)、