电视传媒为了解某市100万观众对足球节目的收视情况，随机抽取了100名观众进行调查．如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图，将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”，并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”．
（1）试估算该市“足球迷”的人数，并指出其中“铁杆足球迷”约为多少人；
（2）该市要举办一场足球比赛，已知该市的足球场可容纳10万名观众．根据调查，如果票价定为100元/张，则非“足球迷”均不会到现场观看，而“足球迷”均愿意前往现场观看．如果票价提高
元/张
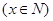，则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
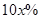，“铁杆足球迷”愿意前往观看的人数会减少
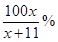．问票价至少定为多少元/张时，才能使前往现场观看足球比赛的人数不超过10万人？
已知二次函数
对任意
，都有
成立，设向量
（sinx，2），
（2sinx，
），
（cos2x，1），
（1，2），当
[0，
]时，求不等式f（
）＞f（
）的解集．
．(本题满分14分)已知函数f(x)＝sin(ωx＋φ)，其中ω>0，|φ|<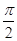
.
(1)若cos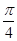
cosφ－sin
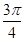sinφ＝0，求φ的值；
(2)在(1)的条件下，若函数f(x)的图象的相邻两条对称轴之间的距离等于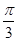
，求函数f(x)的解析式；并求最小正实数m，使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数．
(本题满分12分)设函数f(x)＝a·b，其中向量a＝(2cosx,1)，b＝(cosx，
sin2x＋m)．
(1)求函数f(x)的最小正周期和在[0，π]上的单调递增区间．
(2)当x∈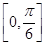
时，－4<f(x)<4恒成立，求实数m的取值范围．
(本小题满分12分)设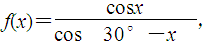
，
（1）求f(x)＋f(60°－x)（2）求f(1°)＋f(2°)＋…＋f(59°)的值
．(本题满分12分)若关于x的方程x2＋2ax＋2－a＝0有两个不相等的实根，求分别满足下列条件的a的取值范围．
(1)方程两根都小于1；
(2)方程一根大于2，另一根小于2.