植树节前夕,某校所有学生参加植树活动,要求每人植2~6棵.活动结束后,校学生会就本校学生的植树量进行了调查.经过对调查数据的分析,得到如下图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题: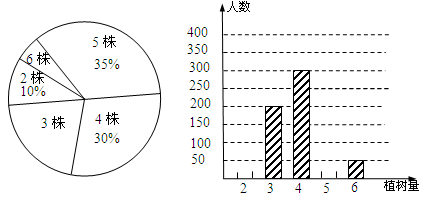
(1)求该校共有多少名学生;
(2)将条形统计图补充完整;
(3)在扇形统计图中,计算出“3棵”部分所对应的圆心角的度数;
(4)在这次调查中,众数和中位数分别为多少?
(5)从该校中任选一名学生,其植树量为“6棵”的概率是多少?
判断下列命题的真假:
(1)一个三角形如果有两个角互余,那么这个三角形是直角三角形;
(2)如果│a│=│b│,那么a3=b3.
写出下列命题的条件和结论:
(1)两条直线被第三条直线所截,同旁内角互补;
(2)如果两个三角形全等,那么它们对应边上的高也相等.
如图,在平行四边形中,DF⊥AC于F,BE⊥AC于E,试问DF与BE的位置关系和数量关系如何?你能肯定吗?请说明理由.
观察下列各式,: ×2=
×2= +2;
+2;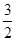 ×3=
×3=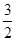 +3;
+3; ×4=
×4= +4;
+4; ×5=
×5= +5;……
+5;……
想一想:什么样的两个数之积等于这两个数的和?设n表示正整数,用关于n的代数式表示这个规律为:×= +.你能说明吗?
平行四边形ABCD中,E,F分别为BC,AD中点,连接AE,CF,试问四边形AECF是什么四边形?你能肯定吗?请说明理由.