[2012·湖北高考]过点P(1,1)的直线,将圆形区域{(x,y)|x2+y2≤4}分成两部分,使得这两部分的面积之差最大,则该直线的方程为( )
| A.x+y-2=0 | B.y-1=0 |
| C.x-y=0 | D.x+3y-4=0 |
已知集合M={x|x2-2008x-2009>0},N={x|x2+ax+b≤0},若M∪N=R,M∩N=(2009,2010],则
A.a="2009,b=-2010" B.a=-2009,b=2010
C.a="2009,b=2010" D.a=-2009,b=-2010
已知复数 =2+i,
=2+i,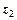 =3-i,其中i是虚数单位,则复数
=3-i,其中i是虚数单位,则复数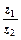 的实部与虚部之和为()
的实部与虚部之和为()
| A.0 | B.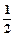 |
C.1 | D.2 |
设函数 是奇函数,并且在R
是奇函数,并且在R 上为增函数,若0≤
上为增函数,若0≤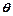 ≤
≤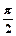 时,f(msin
时,f(msin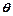 )+f(1—m)>0恒成立,则实数m的取值范围是( )
)+f(1—m)>0恒成立,则实数m的取值范围是( )
| A.(0,1) | B.(-∞,0) | C. |
D.(-∞,1) |
已知双曲线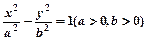 的左、右焦点分别为F1、F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为( )
的左、右焦点分别为F1、F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为( )
A.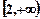 B.
B.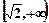 C
C .
. D.
D.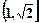
.已知复数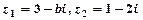 ,若
,若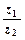 是实数,则实数b的值为()
是实数,则实数b的值为()
| A.6 | B.-6 | C.0 | D.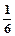 |