一带电粒子无初速度的进入一加速电场A,然后垂直进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),如图所示。已知加速电场A板间电压为U1,M、N两板间的电压为U2,两板间的距离为d,板长为L,粒子的质量为m,电荷量为q,不计粒子受到的重力及它们之间的相互作用力。求: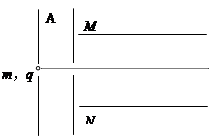
(1)粒子穿过A板时速度大小v0;
(2)粒子从偏转电场射出时的侧移量y;
(3)粒子从偏转电场射出时速度的偏转角q
如图所示,小球A质量为m,固定在长为L的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直平面内做圆周运动。当小球经过最高点时,杆对球产生向下的拉力,拉力大小等于球的重力。
求:(1)小球到达最高时速度的大小。
(2)当小球经过最低点时速度为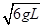 ,杆对球的作用力的大小。
,杆对球的作用力的大小。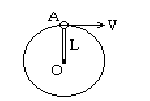
2008年9月,神舟七号载人航天飞行获得了圆满成功,我国航天员首次成功实施空间出舱活动、飞船首次成功实施释放小伴星的实验,实现了我国空间技术发展的重大跨越。已知飞船在地球上空的圆轨道上运行时离地面的高度为h。地球半径为R,地球表面的重力加速度为g。求飞船在该圆轨道上运行时的速度v和周期T。
如图所示,在光滑水平面上有质量均为m的两辆小车A和B,A车上表面光
滑水平、其上表面左端有一质量为M的小物块C(可看作质点).B车上表面是一个光滑的 圆弧槽,圆弧槽底端的切线与A的上表面相平.现在A和C以共同速度v0冲向静止的B
圆弧槽,圆弧槽底端的切线与A的上表面相平.现在A和C以共同速度v0冲向静止的B
车,A、B碰后粘合在一起,之后物块C滑离A,恰好能到达B的圆弧槽的最高点.已知M=2m,
v0=4.0m/s,取g=10m/s2.求圆弧槽的半径R.

如图所示,在坐标系的第一象限内有一横截面为四分之一圆周的柱状玻璃体
OPQ,OP=OQ=R,一束单色光垂直OP面射入玻璃体,在
OP面上的入射点为A,OA=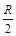 ,此单色光通过玻璃体后沿BD
,此单色光通过玻璃体后沿BD
方向射出,且与x轴交于D点,OD= ,求:
,求:
①该玻璃的折射率是多少?
②将OP面上的该单色光至少向上平移多少,它将不能从PQ面直接折射出来。
某同学家新买了一双门电冰箱,冷藏室容积107 L,冷冻容积118 L,假设室内空气为理想气体。
①若室内空气摩尔体积为 ,阿伏加德罗常数为
,阿伏加德罗常数为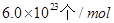 ,在家中关闭冰箱密封门后,电冰箱的冷藏室和冷冻室内大约共有多少个空气分子?
,在家中关闭冰箱密封门后,电冰箱的冷藏室和冷冻室内大约共有多少个空气分子?
②若室内温度为27℃,大气压为l×105 Pa,关闭冰箱密封门通电工作一段时间后,冷藏室内温度降为6℃,冷冻室温度降为-9℃,此时冷藏室与冷冻室中空气的压强差为多大?
③冰箱工作时把热量从温度较低的冰箱内部传到温度较高的冰箱外部,请分析说明这是否违背热力学第二定律。