如图所示,半径R = 0.1m的竖直半圆形光滑轨道bc与水平面ab相切。质量m = 0.1kg的小滑块B放在半圆形轨道末端的b点,另一质量也为m= 0.1kg的小滑块A,以v0 = 2 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求:
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求:

(1)A与B碰撞前瞬间的速度大小vA;
(2)碰后瞬间,A、B共同的速度大小v;
(3)在半圆形轨道的最高点c,轨道对A、B的作用力N的大小。
灵巧、省力的电动自行车,最近几年已成为人们出行的主要交通公具。下表为一辆电动自行车的铭牌上给出的技术参数。请利用表中数据进行计算:(取g=10m/s2)
| 规格 |
后轮驱动直流电机 |
||
| 车型 |
26英寸 |
额定输出功率 |
160W |
| 整车质量 |
40kg |
额定电压 |
40V |
| 最大载量 |
120kg |
额定电流 |
5.0A |
(1)电动机以额定值正常工作时的机械效率。
(2)在额定电压下,电机突然卡死时,电机的总功率。
(3)当自行车以额定功率在平直公路上满载匀速行驶时,若其受到的阻力为总重量的0.02倍,则此时其速度为多少?
(本题12分)如图所示,条形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场,磁感应强度B的大小均为0.3T,AA′、BB′、CC′、DD′为磁场边界,它们相互平行,条形区域的长度足够长,磁场宽度及BB′、CC′之间的距离d=1m。一束带正电的某种粒子从AA′上的O点以沿与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v0时,粒子在区域Ⅰ内的运动时间均为t0=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ。取π≈3,不计粒子所受重力。 求:
(1)粒子的比荷q/m;⑵速度v0和v1的大小;⑶速度为v1的粒子从O到DD′所用的时间。
(本题10分)如图所示,某空间有一竖直向下的匀强电场,电场强度E,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h的a处有一微粒源,盒内微粒以 的初速度向水平面以下的各个方向均匀放出质量为m,电荷量为q的带正电微粒,粒子最终落在金属板b上。(要考虑微粒的重力,阻力不计)求:
的初速度向水平面以下的各个方向均匀放出质量为m,电荷量为q的带正电微粒,粒子最终落在金属板b上。(要考虑微粒的重力,阻力不计)求:
(1)微粒源所在处a点的电势?
(2)带电微粒打在金属板上时的动能?
(3)从微粒源射出的粒子打在金属板上的范围(所形成的面积)?若使带电微粒打在金属板上的范围增大,可以通过改变哪些物理量来实现?(至少答两种)
(本题6分)如图所示,水平向右的匀强电场场强为E,有一绝缘轻细杆长为l,一端可绕O点在竖直面内无摩擦转动,另一端粘有一带正电荷的小球,电量为q,质量为m,将小球拉成与O点等高的A点后自由释放,求小球到达最低点B时绝缘杆给小球的力。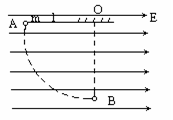
如图所示,在国庆阅兵式中,某直升飞机在地面上空某高度A位置处于静止状态待命,要求该机10时56分40秒由静止状态沿水平方向做匀加速直线运动,经过AB段加速后,进入BC段的匀速受阅区,11时准时通过C位置,如下图所示,已知xAB=5 km,xBC=10 km.问: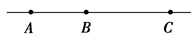
(1)直升飞机在BC段的速度大小是多少?
(2)在AB段做匀加速直线运动时的加速度大小是多少?