如图所示，质量为m、电荷量为q的带负电粒子（不计重力）。由0点静止释放进入宽为L的匀强电场，经电压为U加速后又进入磁感应强度为B的匀强磁场，磁场区域如图所示。
（1）带电粒子进入磁场时的速度大小；
（2）若带点粒子能够再次返回入射边界，则磁场的最小宽度为多大；
（3）若满足（2）的条件，则带点粒子在电场和磁场中运动的总时间为多少。
如图为修建高层建筑常用的塔式起重机.在起重机将质量m＝5×103 kg的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加速度a＝0.2 m/s2，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做vm＝1.02 m/s的匀速运动.取g＝10 m/s2，不计额外功.求：
(1)起重机允许输出的最大功率；
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率.
两个星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动，现测得两个星球中心距离为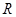
，其运动周期为
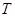，万有引力常量为
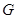，求两个星球的总质量。
已知地球半径为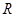
=6400km，地面上重力加速度
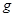="9.80" m/s2，万有引力常量
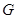=6.67×10-11N·m2/kg2，如不考虑地球自转影响，求地球的平均密度表达式及大小。（大小结果保留两位有效数字）
有两滑块AB置于光滑的水平面上，A的质量为m，B的质量为2m，在水平面的右侧有一粗糙的斜面，斜面很长且倾角为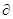
，A、B两物体与斜面的动摩擦因素均为
，且最大的静摩擦力等于滑动摩擦力。现突然给A施一水平向右冲量I，A、B碰撞无机械能损失，滑块由水平面运动至斜面也不考虑转弯处的机械能损失。求
1．A受冲量作用后的速度大小？
2．求AB碰后的速度?
3．若AB只发生一次碰撞，求摩擦力对B做功?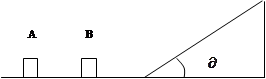
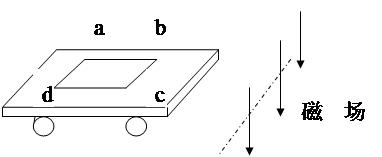
某同学为了探究涡流制动原理，在玩具小车的底部固定了一个水平放置的矩形线圈abcd，小车（含线圈）总质量为4kg，闭合线圈共100匝，线圈长Lab=Lcd=20cm,线圈宽Lbc=Lad=10cm，线圈的电阻为0.5欧，在小车轨道的正前方布置了一个固定的磁场区，磁场的边界始终与线圈bc边平行，磁场的方向竖直向下，磁感应强度B=0.2T，忽略小车与轨道面的摩擦，小车的初速度为2m/s。当线圈刚进入磁场时，求
1线圈中感应电流的大小？
2线圈受安培力的大小？
3小车加速度大小？