如图,四边形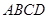 为矩形,四边形
为矩形,四边形 为梯形,
为梯形,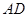 ∥
∥ ,
, ,且平面
,且平面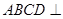 平面
平面 ,
, ,点
,点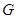 为
为 的中点.
的中点.
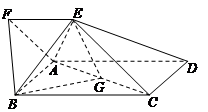
(1)求证: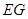 ∥平面
∥平面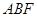 ;
;
(2)求三棱锥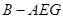 的体积;
的体积;
(3)试判断平面 与平面
与平面 是否垂直?若垂直,请证明;若不垂直,请说明理由.
是否垂直?若垂直,请证明;若不垂直,请说明理由.
(本题12分) 抛物线的顶点在原点,焦点在射线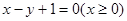
 上
上
(1)求抛物线的标准方程;
(2)过(1)中抛物线的焦点F作动弦AB,过A、B两点分别作抛物线的切线,设其交点为M,求点M的轨迹方程,并求出 的值.
的值.
(本题12分)已知函数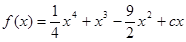 有三个极值点。
有三个极值点。
(1)求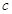 的取值范围
的取值范围
(2)若存在 ,使函数
,使函数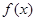 在区间
在区间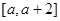 上单调递减,求
上单调递减,求 的取值范围。
的取值范围。
(本题12分)已知函数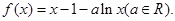
(1)若曲线 在x=1处的切线方程为
在x=1处的切线方程为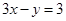 ,求实数a的值;
,求实数a的值;
(2)若 的值域为
的值域为 ,求a的值;
,求a的值;
(本题12分)设有关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若 是从区间
是从区间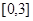 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(本题12分)椭圆C: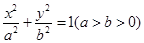 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且 (1)求椭圆C的方程;
(1)求椭圆C的方程;
(2)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于 两点,且A
两点,且A 、B关于点M对称,求直线l的方程.
、B关于点M对称,求直线l的方程.