“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下：如图，P、Q为某地区水平地面上的两点，在P点正下方一球形区域内储藏有石油，假定区域周围岩石均匀分布，密度为；石油密度远小于，可将上述球形区域视为空腔。如果没有这一空腔，则该地区重力加速度（正常值）沿竖直方向；当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向（即PO方向）上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量，常利用P点附近重力加速度反常现象。已知引力常数为G。

（1）“重力探矿”利用了“割补法”原理：如图所示，在一个半径为R、质量为M的均匀球体中，紧贴球的边缘挖去一个半径为R/2的球形空穴后，剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
（2）设球形空腔体积为V，球心深度为d（远小于地球半径），=x，利用“割补法”原理：如果将近地表的球形空腔填满密度为的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值（在OP方向上的分量）
（3）若在水平地面上半径L的范围内发现：重力加速度反常值在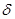与（k>1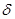）（为常数）之间变化，且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的，试求此球形空腔球心的深度和空腔的体积。

科目 物理   题型 计算题   难度 困难

知识点： 万有引力定律及其应用